1. [latex]{\sigma}_{x}, {\sigma}_{y} and {\tau}_{xy}[/latex] are rectangular stress components at a point. The radius of Mohr’s circle is

A. [latex]\sqrt{{{\sigma}_{x}}^{2} - {{\sigma}_{y}}^{2} + {{\tau}_{xy}}^{2}} [/latex] B. [latex]\sqrt{{(\frac{{\sigma}_{y} + {\sigma}_{x}}{2}})^{2} + {{\tau}_{xy}}^{2}} [/latex] C. [latex]\sqrt{{{\sigma}_{y}}^{2} - {{\sigma}_{x}}^{2} + {{\tau}_{xy}}^{2}} [/latex] D. [latex]\sqrt{{(\frac{{\sigma}_{y} - {\sigma}_{x}}{2}})^{2} + {{\tau}_{xy}}^{2}} [/latex]

Answer - Option D
2. The maximum allowable compressive stress corresponding to lateral buckling in a discretely laterally supported symmetrical I-beam, does not depend upon

A. modulus of elasticity B. radius of gyration about the minor axis C. span/length of the beam D. ratio of overall depth to thickness of the flange

Answer - Option A
Explanation -
Since allowable compressive stress depends upon [latex]\frac{D}{T}[/latex] ratio and [latex]\frac{I}{{r}_{y}}[/latex] ratio as per I.S. Code 800 : 1984. Therefore, it will not depend upon the modulus of elasticity
3. The value of the maximum shear stress will be

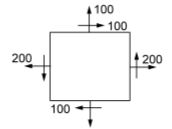
A. [latex]25 \sqrt{5} [/latex] B. [latex]50 \sqrt{5} [/latex] C. [latex]100 \sqrt{5} [/latex] D. [latex]200 \sqrt{5} [/latex]

Answer - Option
Explanation -
[latex]{\sigma}_{x} = 200, {\sigma}_{Y} = 100 and {\tau}_{xy} = 100[/latex]
[latex]{\sigma}_{P1}, {\sigma}_{P2} = \frac{{\sigma}_{y} + {\sigma}_{x}}{2} \pm \sqrt{{(\frac{{\sigma}_{y} + {\sigma}_{x}}{2}})^{2} + {{\tau}_{xy}}^{2}} [/latex]
[latex]\frac{200 + 100}{2}\pm \sqrt{{(\frac{200 - 100}{2})}^{2} + {100}^{2}}[/latex]
[latex]= 150 \pm\sqrt {{50}^{2} + {100}^{2}} = 150 \pm 50 \sqrt {5}[/latex]
[latex]= 150 + 50 \sqrt{5}, 150 - 50 \sqrt{5}[/latex]
[latex]{\sigma}_{P1} = 150 + 50 \sqrt{5}[/latex]
[latex]{\sigma}_{P2} = 150 - 50 \sqrt{5}[/latex]
Also [latex]{\tau}_{max} = \frac{{\sigma}_{Pmax} - {\sigma}_{Pmin}}{2} = 50 \sqrt{5}[/latex]
This is maximum in plane shear stress.
4. The buckling load in a steel column is

A. related to the length B. directly proportional to the slenderness ratio C. inversely proportional to the slenderness ratio D. non-linearly to the slenderness ratio

Answer - Option A
Explanation -
[latex]{P}_{er} = \frac{{\pi}^{2} EI}{{I}^{2}} = \frac{{\pi}^{2}EA{r}^{2}}{{I}^{2}}[/latex]
[latex]= \frac{{\pi}^{2}EA}{{(\frac{I}{r})}^{2}} = \frac{{\pi}^{2}EA{r}^{2}}{{(slenderness ratio)}^{2}}[/latex]
[latex]{P}_{er}[/latex] could be non linearly related to slenderness ratio so better to avoid choice (d).
5. If the principal stress corresponding to a two dimensional state of stress are [latex]{\sigma}_{1} and {\sigma}_{2} and {\sigma}_{1}[/latex] is greater than [latex]{\sigma}_{2}[/latex] and both are tensile, then which one of the following would be the correct criterion for failure by yielding, according to the maximum shear stress criterion ?

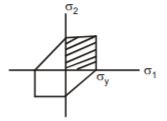
A. [latex]\frac {{\sigma}_{1} - {\sigma}_{2}}{2} = \pm \frac{{\sigma}_{yp}}{2}[/latex] B. [latex] \frac{{\sigma}_{1}}{2} = \pm \frac{{\sigma}_{yp}}{2}[/latex] C. [latex] \frac{{\sigma}_{2}}{2} = \pm \frac{{\sigma}_{yp}}{2}[/latex] D. [latex] {\sigma}_{1} = \pm 2{\sigma}_{yp}[/latex]

Answer - Option A
Explanation -

[latex] {\sigma}_{1} > {\sigma}_{2}[/latex]
Maximum Shear Stress Theory
Maximum Shear Stress = [latex]\frac{{\sigma}_{max} - {\sigma}_{min}}{2}[/latex]
= [latex]\frac{{\sigma}_{1} - 0}{2} = \frac{{\sigma}_{1}}{2}[/latex]
Criterion = [latex] \frac{{\sigma}_{1}}{2} = \pm \frac{{\sigma}_{yp}}{2}[/latex]
6. Consider the following statements :
In a uni-dimensional stress system, the principal plane is defined as one on which the

1. Shear stress is zero 2. Normal stress is zero 3. Shear stress is maximum 4. Normal stress is maximum

Of these statements :

A. 1 and 2 are correct B. 2 and 3 are correct C. 1 and 4 are correct D. 3 and 4 are correct

Answer - Option C
Explanation -
Only (1) can be correct
(4) also Satisfies
[latex]\Rightarrow[/latex] correct statement is (1) and (4)
7. A Mohr’s circle reduces to a point when the body is subjected to

A. pure shear B. uni-axial stress only C. equal and opposite axial stresses on two mutually perpendicular planes, the planes being free of shear D. equal axial stresses on two mutually perpendicular planes, the planes being free of shear.

Answer - Option D
Explanation -
A Mohr’s circle reduces to a point when the body is subjected to equal axial stresses on two mutually perpendicular planes, the planes being free of shear.
8. The number of strain readings (using strain gauges) needed on a plane surface to determine the principal strains and their directions is

A. 1 B. 2 C. 3 D. 4

Answer - Option C
9. When two mutually perpendicular principal stresses are unequal but alike, the maximum shear stress is represented by

A. the diameter of the Mohr’s circle B. half the diameter of the Mohr’s circle C. one-third the diameter of the Mohr’s circle D. one-fourth the diameter of the Mohr’s circle

Answer - Option B
10. If the value of Poisson’s ratio is zero, then it means that

A. the material is rigid B. the material is perfectly plastic C. there is no longitudinal strain in the material D. none of these

Answer - Option D

1. The plane of maximum shear stress has normal stress that is

A. maximum B. minimum C. zero D. None of these

Answer - Option B
2. When [latex]\sigma[/latex] and Young’s Modulus of Elasticity E remains constant, the energy-absorbing capacity of part subject to dynamic forces, is a function of its

A. length B. cross-section C. volume D. none of these

Answer - Option C
Explanation -
Strain energy, U = [latex]\frac{{\sigma}^{2}}{2E}[/latex]
[latex]\sigma[/latex] and E remaining constant, U is proportional to (A.L.) which is volume.
Also, since U is a function of [latex]{\sigma}^{2}[/latex], that portion of the part which is prone to high localized stresses will absorb a high amount of energy, making it vulnerable to failure, such a part, therefore, is designed to have such a contour that, when it is subjected to time-varying or impact loads or other types of dynamic forces, the part absorbs or less uniform stress distribution along the whole length of the part is whole length of the part is ensured.
3. The shear stress distribution over a rectangular cross-section of a beam follows

A. a straight line path B. a circular path C. a parabolic path D. an elliptical path

Answer - Option C
Explanation - A parabolic path

4. When a column is fixed at both ends, corresponding Euler’s critical load is

A. [latex]\frac{{\pi}^{2} EI}{{L}^{2}}[/latex] B. [latex]\frac{2 {\pi}^{2} EI}{{L}^{2}}[/latex] C. [latex]\frac{3 {\pi}^{2} EI}{{L}^{2}}[/latex] D. [latex]\frac{4 {\pi}^{2} EI}{{L}^{2}}[/latex]

Answer - Option D
Explanation -
Euler’s critical load, P = [latex]\frac{{\pi}^{2} EI}{{{L}_{eff}}^{2}}[/latex]
where,[latex]{L}_{eff}[/latex] = effective length of the column.
When both ends are fixed,
[latex]{L}_{eff}[/latex] = 0.5 L
[latex]{P}_{cr} = \frac{{\pi}^{2} EI}{{(0.5 L)}^{2}} = \frac{{\pi}^{2}EI{r}^{2}}{{(0.25 L)}^{2}} or \frac{4{\pi}^{2}EI{r}^{2}}{{L}^{2}}[/latex]
5. For the two shafts connected in parallel, find which statement is true ?

A. Torque in each shaft is the same B. Shear stress in each shaft is the same C. Angle of twist of each shaft is the same D. Torsional stiffness of each shift is the same

Answer - Option C
6. The slenderness ratio of a compression member is :

A. [latex]\frac{Effective length}{Least radius of gyration}[/latex] B. [latex]\frac{Actual length}{Moment of inertia}[/latex] C. [latex]\frac{Moment of inertia}{Actual length}[/latex] D. [latex]\frac{Actual length}{Radius of gyration}[/latex]

Answer - Option A
Explanation -
Slenderness ratio is the ratio of the length of a column and the least radius of gyration of its cross section. Often denoted by lambda. It is used extensively for finding out the design load as well as in classifying various columns in short /intermediate/long.
7. The length of a bar is L metres. It extends by 2 mm when a tensile force F is applied. Find the strain produced in the bar :

A. [latex]\frac{0.002}{L}[/latex] B. [latex]\frac{2}{L}[/latex] C. [latex]\frac{0.2}{L}[/latex] D. [latex]\frac{L}{0.002}[/latex]

Answer - Option A
8. For perfectly elastic bodies, the value of coefficient of restitution is :

A. 0 B. 0.5 C. 1.0 D. 0.25

Answer - Option C
Explanation -
The coefficient of restitution (COR) is the ratio of the final to initial relative velocity between two objects after they collide. It normally ranges from 0 to 1 where 1 would be a perfectly elastic collision.
9. Choose the option which correctly shows the relationship between Modulus of Elasticity (E); Modulus of Rigidity (c) and Bulk Modulus (K) :

A. [latex]E = \frac{KC}{K + C}[/latex] B. [latex]E = \frac{2KC}{2K + C}[/latex] C. [latex]E = \frac{9KC}{3K + C}[/latex] D. [latex]E = \frac{3KC}{K + 2C}[/latex]

Answer - Option C
Explanation -
We know that,
E = 2C(1 + [latex]\mu[/latex]) ...(i)
and E = 3K (1 – 2 [latex]\mu[/latex]) ...(ii)
From (i)
1 + [latex]\mu = \frac{E}{2C}[/latex]
i.e, [latex]\mu \frac{E}{2C} - 1[/latex]
Equating this value in (i)
E = 3K[1 - 2( [latex]\frac{E}{2C} - 1)] = 3K[1 - \frac{E}{C} + 2][/latex]
E = 3K[3 - ( [latex]\frac{E}{C})] = 3K[\frac{3C - E}{C}][/latex]
EC = 3K(3C – E) = 9KC – 3KE
i.e, EC + 3KE = 9KC
i.e, E (C + 3K) = 9KC
i.e, E = [latex]\frac{9KC}{C + 3K}[/latex]
10. The property of a material by which it can be rolled into sheets is called :

A. Elasticity B. Plasticity C. Ductility D. Malleability

Answer - Option D
Explanation -
Malleability is a substance's ability to deform under pressure (compression stress). If malleable, a material may be flattened into thin sheets by hammering or rolling. Malleable materials can be flattened into metal leaf. Many metals with high malleability also have high ductility.
11. A simply supported beam of length L is loaded with a uniformly distributed load of [latex]\omega[/latex] per unit length. The maximum bending moment will be :

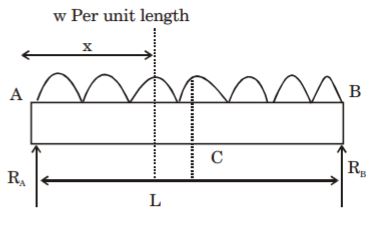
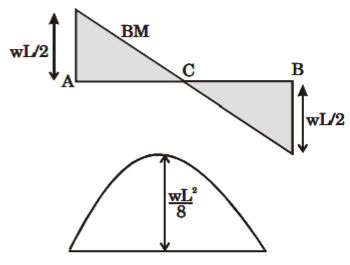
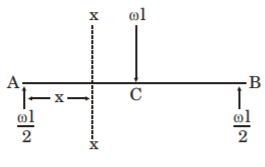
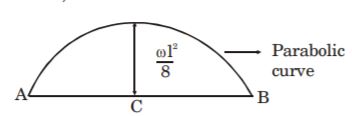
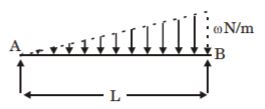
A. [latex]\frac{\omega{L}^{2}}{4}[/latex] B. [latex]\frac{\omega{L}^{2}}{8}[/latex] C. [latex]\frac{\omega{L}^{2}}{2}[/latex] D. [latex]\omega{L}^{2}[/latex]

Answer - Option B
Explanation -
SF and BM Formulas
Simply supported with uniform distributed load
Fx = Shear force at X
Mx = Bending Moment at X
[latex]
[latex]
12. Which of the following property is generally NOT shown by metal ?

A. Electrical conduction B. Sonorous in nature C. dullness D. ductility

Answer - Option C
Explanation -
Dullness is the property which is not shown by the metal.

1. In S.I system, unit of stress is:

A. [latex]\frac{kg}{{cm}^{2}}[/latex] B. N C. [latex]\frac{N}{{m}^{2}}[/latex] D. Watt

Answer - Option C
Explanation -
The S.I. unit of stress is [latex]\frac{N}{{m}^{2}}[/latex].
2. What is the function of push rod in a diesel engine? It transfers force between -

A. Cam and rocker arm B. Connecting rod and piston C. Crankshaft and piston D. None of these

Answer - Option A
Explanation - A push rod is a component of the valve train of certain piston engines. It's function is essentially to push the valve open. Rods used in an overhead valve engine to open and close the valves. One end is pushed up by the cam and other end makes contact with the rocker arms which rotates and pushes the valve open.
3. . In C.G.S system, the unit of strain is:

A. [latex]\frac{cm}{kg}[/latex] B. [latex]\frac{m}{kg}[/latex] C. no units D. None of these

Answer - Option C
Explanation -
Strain is unit less quantity. It is dimensionless.
4. In the case of a uniformly distributed load on a simply supported beam, the bending moment diagram would be-

A. 1 B. 2 C. 3 D. 4

Answer - Option B
Explanation -
Simply supported beam with udl,

Now FBD, take sagging (+ve) and hogging (– ve),

Now, [latex]{M}_{x} = \frac{\omega l}{2}x - \omega x \frac{x}{2}[/latex]
[latex]{M}_{x} = \frac{\omega l}{2}x - \omega x \frac{{x}^{2}}{2}[/latex]
[latex]{M}_{A} = ({A}^{B}x = L)[/latex]
[latex]\omega x \frac{{x}^{2}}{2} - \omega x \frac{{x}^{2}}{2} = 0[/latex]
For maximum bending
[latex]\frac{d {M}_{X}}{dx} = \frac{\omega l}{2} - \omega = 0[/latex]
Now, x = [latex]\frac{1}{2}[/latex], so bending moment at x = [latex]\frac{1}{2}[/latex] to be maximum so,
Mc = [latex]\frac{\omega l}{2} * \frac{l}{2} - \frac{\omega {(\frac{l}{2})}^{2}}{2} = \frac{\omega{l}^{2}}{4} - \frac{\omega{l}^{2}}{8} = \frac{\omega{l}^{2}}{8}[/latex]
Mc = [latex]\frac{\omega{l}^{2}}{8}[/latex]
Hence, BMD should be

So, option (b) is correct.
5. A simply supported beam carries a varying load from zero at one end to [latex]\omega[/latex] N/m at the other end (as under).

The length of the beam is L. The shear force will be zero at a distance 'x' from A. Find 'x' :

A. [latex]\frac{L}{2}[/latex] B. [latex]\frac{L}{4}[/latex] C. [latex]\frac{L}{\sqrt{3}}[/latex] D. [latex]\frac{L}{3}[/latex]

Answer - Option C
Explanation -

By FBD,

Load at point C = [latex]\frac{WL}{2}[/latex]
Now, [latex]\Sigma {M}_{B} = 0[/latex]
[latex]{R}_{A} * L = \frac{WL}{2} * \frac{L}{3}[/latex]
[latex]{R}_{A} = \frac{WL}{6}[/latex]
Here, from similar [latex]\Delta[/latex] AXX and AWB,
[latex]\frac{{W}_{xx}}{W} = \frac{x}{L}\Rightarrow {W}_{xx} = \frac{{W}_{x}}{L} [/latex]
Shear force at X– X cross section,
[latex]{SF at}_{xx} = \frac{WL}{6} - \frac{1}{2} * {W}_{xx} * x [/latex]
[latex]\frac{WL}{6} - \frac{1}{2} * \frac{Wx}{L} * x[/latex]
[latex]\frac{WL}{6} - \frac{1}{2} * - \frac{W{x}^{2}}{L}[/latex]
SF at X-X section = 0 [By question]
[latex]0 = \frac{WL}{6} - \frac{W{x}^{2}}{2L}[/latex]
[latex]\frac{WL}{6} = \frac{W{x}^{2}}{2L}[/latex]
[latex]\Rightarrow {x}^{2} = \frac{2{L}^{2}}{6} = \frac{{L}^{2}}{3}[/latex]
[latex]\Rightarrow x = \frac{1}{\sqrt{3}}[/latex]
6. Which one of the following is the most significant property to be considered in the selection of material for the manufacture of locating pins and drill jig bushes used in jigs and fixtures ?

A. Wear Resistance B. Elasticity C. Shear Strength D. Tensile Strength

Answer - Option D
Explanation -
Tensile strength is the criteria for selection of material in manufacturing of locating pins and jug bushes.
7. What is the main shaft of an engine that controls the movement of piston ?

A. axle B. drive shaft C. crank shaft D. cam shaft

Answer - Option C
8. The component of the engine that connects the link between the small end of the connecting rod and the piston is known as

A. Cams B. Fly wheel C. Gudgeon pin D.

Answer - Option C
Explanation -
Gudgeon pin is defined as the pin which holds piston rod and connecting rod together.
9. The negative ratio of transverse to axial strain is called as

A. Young's modulus B. Shear modulus C. Poisson's ratio D. Bulk modulus of elasticity

Answer - Option C
Explanation -
Poisson’s ratio: Poisson’s ratio is the ratio of transverse contraction strain to longitudinal extension strain in the direction of stretching force. Tensile deformation is considered positive and compressive deformation is considered negative.
10. To connect piston to the connecting rod the_______ are used

A. rod caps B. cap bolts C. small end bearings D. gudgeon pins

Answer - Option D
Explanation -
Gudgeon pins are those pins which holds piston and connecting rod together.