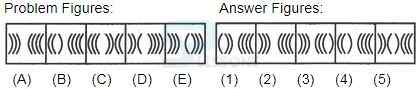
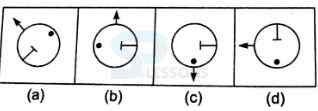
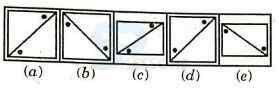
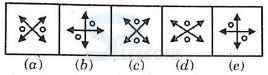
Introduction
Introduction
SSC Selection Post Phase VIII – First Stage CBT, conducted in online Mode, has: a duration of 1 hour [1 hour 20 Minutes for eligible PwBD candidates accompanied with Scribe], a maximum score of 200 marks and consists of 4 sections, namely – Reasoning, English Language, Quantitative Aptitude (Basic Arithmetic Skill) and General Awareness. The 4 sections are not separately timed. There is a Negative marking in SSC Selection Post Phase VIII First Stage CBT and 0.50 marks are deducted for each wrong answer. The below sections gives the detailed information about SSC Selection Post Phase VII Model Paper 1.
SSC Selection Post Phase VIII Selection Process shall involve three stages: Paper-I - Computer Based Examination and Document Verification (DV). Selection is made strictly as per merit, on the basis of all recruitment stages.
 Exam Pattern
Exam Pattern
| SSC Selection Post Phase VIII Model Paper 1 - Exam Pattern | ||||
|---|---|---|---|---|
| S.No | Name Of Test | No.of Questions | Maximum Marks | Duration |
| 1. | Reasoning | 25 | 50 | 60 Minutes (80 minutes for candidates eligible for scribes |
| 2. | English Language | 25 | 50 | |
| 3. | Quantitative Aptitude (Basic Arithmetic Skill) | 25 | 50 | |
| 4. | General Awareness | 25 | 50 | |
| Total | 100 | 200 | 60 Minutes | |
Note:
- There will be negative marking of 0.50 marks for each wrong answer.
- Skill Tests like Typing/ Data Entry/ Computer Proficiency Test, etc., where prescribed in the Essential Qualification, will be conducted, which will be of a qualifying nature.
 Syllabus
Syllabus
Indicative Syllabus for Computer Based Examination:
| SSC Selection Post Phase VIII Selection Process - Matriculation level | |
|---|---|
| Subjects | Topics |
| General Intelligence |
|
| English Language |
|
| Quantitative Aptitude |
|
| General Awareness |
|
 Model Paper
Model Paper
Direction(1-3): Each question presents a situation and asks you to make a judgment regarding that particular circumstance. Choose an answer based on given information.
1. Mrs. Jansen recently moved to Arizona. She wants to fill her new backyard with flowering plants. Although she is an experienced gardener, she isn't very well-versed in what plants will do well in the Arizona climate. Also, there is a big tree in her backyard making for shady conditions and she isn't sure what plants will thrive without much direct sunlight. Her favorite gardening catalog offers several backyard seed packages. Which one should Mrs. Jansen choose?
- A. The Rainbow Collection is ideal for North-east gardens. It includes a variety of colorful perennials that thrive in cool, moist conditions.
B. The Greenhouse Collection will blossom year after year if planted in brightly lit locations and watered regularly.
C. The Treehouse Collection will provide lush green plants with delicate colorful flowers that thrive in shady and partially shady locations.
D. The Oasis Collection includes a variety of perennials that thrive in dry climates and bright sunlight.
- A. Marilyn has been a hygienist for fifteen years, and her current employer, who is about to retire, says she is the best in the business. The clientele she has worked with consists of some of the wealthiest and most powerful citizens in the county
B. Lindy recently graduated at the top of her class from one of the best dental hygiene programs in the state. Prior to becoming a dental hygienist, Lindy spent two years working in a day care center.
C. James has worked as a dental hygienist for three years in a public health clinic. He is very interested in securing a position in a private dental office
D. Kathy is an experienced and highly recommended dental hygienist who is also finishing up a degree in early childhood education, which she hopes will get her a job as a preschool teacher. She is eager to find a job in a pediatric practice, since she has always wanted to work with children.
- A. making coupons available that entitle the coupon holder to receive a 25% discount on wedding, anniversary, or birthday cakes
B. exhibiting at the next Bridal Expo and having pieces of one of her wedding cakes available for tasting
C. placing a series of ads in the local newspaper that advertise the wide array of breads
D. moving the bakery to the other side of town
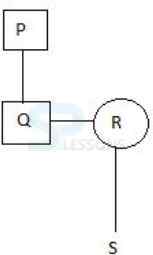
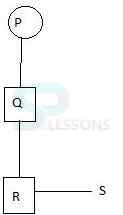
- A. Q is the aunt of R
B. Q is the brother of R
C. Q is the mother of R
D. Q is the father of R
- A. Grandfather
B. mother
C. grandmother
D. father
- A. 30 rolls
B. 58 rolls
C. 120 rolls
D. 150 rolls
- A. 4 p.m
B. 5 p.m
C. 6 p.m
D. 8 p.m
- A. Ring finger
B. Middle finger
C. Thumb
D. Index finger
- A. 2 hours
B. 3 hours
C. 4 hours
D. 5 hours
- A. 1
B. 2
C. 3
D. 4
- A. 1
B. 2
C. 3
D. 4
- A. 1
B. 2
C. 3
D. 4
- A. a
B. b
C. c
D. d
- A. a
B. b
C. c
D. d
- A. 1
B. 2
C. 3
D. 4
- A. 20
B. 18
C. 28
D. 29
- A. 12
B. 10
C. 20
D. 14
- A. a
B. b
C. c
D. d
- A. 7
B. 10
C. 12
D. 13
- A. 20
B. 22
C. 23
D. 26
- A. 22
B. 24
C. 25
D. 26
- A. Only I follow
B. Only II follow
C. Both I and II follow
D. Both II and III follow
- A. If only assumption I is implicit.
B. If only assumption II is implicit.
C. If only assumption III is implicit.
D. If both I and II are implicit.
- A. and
B. Either ‘of’ or ‘development’
C. taxes
D. to
- A. zm ht
B. bt zm
C. ht co
D. br ht
Direction(1-5): Direction: Below is given a single word with four alternatives mentioned after it. You have to select all those alternatives which are synonyms of the word in different contexts. Select the correct alternatives and then mark the correct combination from the options.
1. Stoop
1.To submit
2. To bend the body
3. a small porch.
4. To degrade oneself
- A. 1, 2, 3
B. 2, 3, 4
C. 1, 3, 4
D. All of the above
- A. 1 & 3
B. 2 & 4
C. 1, 2 & 3
D. All of the above
- A. 1,2,3
B. 2,3,4
C. 2,4
D. 1,2,4
- A. 1,2,3
B. 2,3,4
C. 1,3,4
D. 2,4
- A. 1 & 2
B. 2, 3 & 4
C. 1, 3 & 4
D. 1, 2 & 4
- A. though it have time till
B. though this have time until
C. though it has time until
D. No correction required
- A. have it not raise an objection
B. had this not raised an objection
C. had it not raised an objection
D. has it not raised an objection
- A. suffer due to high cost of productions
B. suffers due to high cost production
C. suffers due to high cost of production
D. suffer due to high cost of production
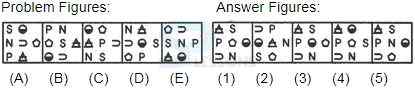
- A. B-D
B. A-C
C. A-D
D. B-C
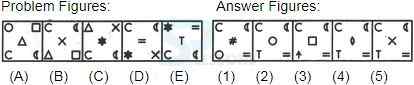
- A. A-B
B. B-C
C. C-D
D. B-D
- A. C-D
B. B-C
C. A-D
D. A-B
- A. B-D
B. A-C
C. B-C
D. A-D
- A. B-C
B. A-D
C. B-D
D. A-C
- A. It is incongruous that the Centre have failed
B. to grasp the need for reform in the
C. regulating of pesticides, when it is
D. focussed on growth in all
- A. The derivative instrument allows investors to enter in contracts
B. to either buy or sell gold sometime in the future on a predetermined
C. price, thus allowing investors for hedge any
D. volatility in the price of the metal
- A. The Centre’s decision to infuse 2.11 lakh crore of fresh
B. capital into public sector banks over the next two
C. years, through a blend of financial
D. All are correct
- A. The theories of logical atomism is a crucial tool in Russell’s
B. philosophy method. Logical atomism contends that,
C. through rigorous and exacting analysis,
D. language like physical matter could be broken down
- A. While Amur tiger occurs exclusively in sub-temperate and
B. snow-covered habitats, the Bengal tigers occupies
C. diverse tropical habitats ranged from Himalayan
D. foothills to Central Indian plateau
- A. I was not averse to fighting with any boy who challenged me.
B. She had a deep aversion to getting up early in the morning.
C. They were averse to the very idea of going out on a rainy day.
D. He seems to be aversing to hard work
- A. Many urbanites would resent additional competition for school places.
B. I resent the way he sneers at our efforts.
C. She was filled with deep resentment at being passed over for promotion.
D. I resent paying extra for my drink just because it’s in a posey bottle
- A. The heat was unrelenting.
B. The committee rewarded employees for their relentless pursuit to excellence.
C. Her face remained unrelenting severe
D. We will not relent until justice is done to the aggrieved.
- A. Try to reduce redundancies in your writings.
B. The company was losing money and it had to make people redundant.
C. The reduntic lyrics made the song unpalatable.
D. The illustration had too much redundant details.
- A. unprecedented
B. assesment
C. overwhelmed
D. devastation
- A. recommendations
B. concessions
C. aggreived
D. revamp
- A. traverce
B. contrarian
C. alliance
D. animosities
1. Can you find the the missing number in the below series
112, 85, 58, X , 4, -23
I. Employees of the given companies can be categorised only in three types:
Engineering Graduates, Science Graduates and Arts Graduates
II. Few values are missing in the table (indicated by ___). A candidate is expected to calculate the missing value, if it is required to answer the given questions, on the basis of the given data and information.
21. What is the difference between the number of Arts graduate employees and Engineering Graduates employees in Company B?
- A. 30
B. 29
C. 33
D. 31
- A. 192
B. 191
C. 195
D. 193
- A. 12, 000
B. 12, 864
C. 15, 600
D. 14, 320
- A. 5200
B. 4000
C. 6500
D. 7800
- A. 168
B. 158
C. 188
D. 198
- A. 618.3
B. 943.2
C. 892.6
D. 764.4
- A. Rs 6020
B. Rs 7860
C. Rs. 7680
D. 7000
- A. 11,000
B. 12,000
C. 10,000
D. 9870
- A. 11000
B. 11250
C. 11500
D. 11550
- A. 500
B. 520
C. 480
D. 400
- A. 500
B. 400
C. 450
D. 600
- A. 775
B. 750
C. 840
D. 850
- A. 90
B. 675
C. 135
D. 450
- A. 432
B. 567
C. 1575
D. 1263
- A. 562
B. 585
C. 650
D. 548
- A. 14
B. 13
C. 12
D. 7
- A. 5.445
B. 5.94
C. 4.95
D. 8.525
- A. 410
B. 450
C. 400
D. 460
- A. 2 days
B. 4 days
C. 5 days
D. 6 days
- A. 4 days
B. 3 days
C. 6 days
D. 5 days
| Company | Total number of Employees | Out of total number of employees | ||
|---|---|---|---|---|
| Percentage of Engineering Graduates | Percentage of Science Graduates | Percentage of Arts Graduates | ||
| A | 1000 | 32% | - | - |
| B | 600 | - | 42% | 30% |
| C | - | 30% | 30% | - |
| D | - | - | 40% | 20% |
| E | - | 35% | 50% | - |
- A. 17
B. 18
C. 12
D. 11
- A. 920
B. 960
C. 1120
D. 1040
- A. 294
B. 266
C. 280
D. 308
- A. 194
B. 166
C. 144
D. 152
- A. 1200
B. 1400
C. 1800
D. 1600
1. Jack Ma stepped down as the Chairman of which among the following companies?
- A. Huawei
B. Alibaba
C. Oppo
D. Xiaomi
- A. September 12th
B. September 15th
C. September 11th
D. September 13th
- A. UNHRC
B. UNSC
C. ICJ
D. UN
- A. Nepal
B. Malaysia
C. Bhutan
D. Bangladesh
- A. Three
B. Five
C. Two
D. Four
- A. Sanjay Mitra Committee
B. Rajnath Singh Committee
C. Amit Shah Committee
D. Ajay Kumar Committee
- A. National Olympic Committee
B. Paralympic Committee of India
C. Empowered Steering Committee
D. Physical education Committee
- A. Prayagraj
B. Gaya
C. Sahibganj
D. Cuttack
- A. Ravindra Bhatt
B. Kalyan Singh
C. Satyadev Narayan Arya
D. Kalraj Mishra
- A. 9th September
B. 10th September
C. 11th September
D. 12th September
- A. K2-18d
B. K2-18c
C. K2-18a
D. K2-18b
- A. PV Sindhu
B. Mary Kom
C. Vinesh Phogat
D. Mithali Raj
- A. China
B. US
C. India
D. Bangladesh
- A. Kempegowda International Airport
B. Cochin International Airport
C. Chhatrapati Shivaji International Airport
D. Indhira Gandhi International Airport
- A. Jharkhand
B. Bihar
C. Uttarakhand
D. Telangana
- A. Cuba
B. St. Vincent and Grenadines
C. St. Lucia
D. Dominican Republic
- A. Odisha
B. Kerala
C. Andhra Pradesh
D. Tamil Nadu
- A. Indonesia
B. Thailand
C. Maldives
D. Singapore
- A. NAG
B. Dhanush
C. Nirbhay
D. MPATGM
- A. Haryana
B. Punjab
C. Madhya Pradesh
D. Tamil Nadu
- A. Ravish Kumar
B. Kiran Bedi
C. Arvind Kejriwal
D. Arnab Goswami
- A. Ladakh and Chandigarh
B. Jammu & Kashmir and Daman and Diu
C. Jammu & Kashmir and Ladakh
D. Jammu & Kashmir and Himachal Pradesh
- A. Ajmal Kasab death penalty case
B. Indira Gandhi Assassination case
C. Rajiv Gandhi assassination case
D. Jessica Lall case
- A. Nepal
B. Malaysia
C. Bhutan
D. Bangladesh
- A. Sanjay Mitra Committee
B. Rajnath Singh Committee
C. Amit Shah Committee
D. Ajay Kumar Committee