Number Systems
1. How many 3 digit number, in all are divisible by 9?

A. 100 B. 99 C. 98 D. 101

Answers: Option (A)
Explanation: The lowest 3-digit no. is 100 and the highest is 999. The lowest 3-digit multiple of 9 is 108, and the highest is 999. No. of multiples in between = [latex]\frac {999−108}{9}[/latex] + 1 = 100
2. Find the remainder when 4[latex]^{13}[/latex] divided by 3?

A. 1 B. 2 C. 0 D. 3

Answers: Option (A)
Explanation: Let us consider 4[latex]^{1}[/latex] = 4, when divided by 3 gives the remainder 1 ⇒ Four power odd number, when divided by 3, gives the remainder 1 Similarly,4[latex]^{3}[/latex]= 64, when divided by 3 gives the remainder 1 ∴ 4[latex]^{13}[/latex] divided by 3 also gives the remainder 1
3. How many numbers less than 1000 are multiples of both 10 and 17?

A. 5 B. 6 C. 7 D. 8

Answers: Option (A)
Explanation: LCM of 10, 17 = 170 We have to find the number of multiples of 170 < 1000 Number of multiples = integer value of (1000/170) = integer part of 5.88 = 5 ∴ there are 5 multiples of both 10 and 17 less than 1000 are 5
4. Which of the following will have the maximum number of factors?

A. 99 B. 101 C. 176 D. 182

Answers: Option (C)
Explanation: Factors of 99 = 1, 3, 9, 11, 33, 99 Factors of 101 = 1, 101 Factors of 176 = 1, 2, 4, 8, 11, 16, 22, 44, 88, 176 Factors of 182 = 1, 2, 7, 13, 14, 26, 91, 182 Thus 176 has the maximum number of factors.
5. A number, when divided by 6 leaves, remainder 3. When the square of the same number is divided by 6, the remainder is

A. 0 B. 1 C. 2 D. 3

Answers: Option (D)
Explanation: Let the number be ‘x’ x = 6y + 3 x[latex]^{2}[/latex] = (6y + 3)[latex]^{2}[/latex] x[latex]^{2}[/latex] = 36y[latex]^{2}[/latex] + 36y + 9 x[latex]^{2}[/latex] = 6 × (6y[latex]^{2}[/latex] + 6y + 1) + 3 ∴ When the square of the same number is divided by 6, the remainder will be 3.
Computation of Whole Numbers
1. 5358 x 51 = ?

A. 273258 B. 273268 C. 273348 D. 273358

Answers: Option (A)
Explanation: 5358 x 51 = 5358 x (50 + 1) = 5358 x 50 + 5358 x 1 = 267900 + 5358 = 273258.
2. The difference of two numbers is 1365. On dividing the larger number by the smaller, we get 6 as quotient and the 15 as remainder. What is the smaller number?

A. 240 B. 270 C. 295 D. 360

Answers: Option (B)
Explanation: Let the smaller number be x. Then larger number = (x + 1365). x + 1365 = 6x + 15 5x = 1350 x = 270 Smaller number = 270.
3. Which one of the following numbers is exactly divisible by 11?

A. 235641 B. 245642 C. 315624 D. 415624

Answers: Option (D)
Explanation: (4 + 5 + 2) - (1 + 6 + 3) = 1, not divisible by 11. (2 + 6 + 4) - (4 + 5 + 2) = 1, not divisible by 11. (4 + 6 + 1) - (2 + 5 + 3) = 1, not divisible by 11. (4 + 6 + 1) - (2 + 5 + 4) = 0, So, 415624 is divisible by 11.
4. Which of the following number is divisible by 24?

A. 35718 B. 63810 C. 537804 D. 3125736

Answers: Option (D)
Explanation: 24 = 3 x8, where 3 and 8 co-prime. Clearly, 35718 is not divisible by 8, as 718 is not divisible by 8. Similarly, 63810 is not divisible by 8 and 537804 is not divisible by 8. Consider option (D), Sum of digits = (3 + 1 + 2 + 5 + 7 + 3 + 6) = 27, which is divisible by 3. Also, 736 is divisible by 8. 3125736 is divisible by (3 x 8), i.e., 24.
5. (?) + 3699 + 1985 - 2047 = 31111

A. 34748 B. 27474 C. 30154 D. 27574 E. None of these

Answers: Option (B)
Explanation: x + 3699 + 1985 - 2047 = 31111 => x + 3699 + 1985 = 31111 + 2047 => x + 5684 = 33158 => x = 33158 - 5684 = 27474.
Decimals and Fractions
1. What is difference between biggest and smallest fraction among 2/3, 3/4, 4/5 and 5/6

A. 2/5 B. 3/5 C. 1/6 D. 1/7

Answers: Option (C)
Explanation: 2/3 = .66, 3/4 = .75, 4/5 = .8 and 5/6 = .833 So biggest is 5/6 and smallest is 2/3 Their difference is 5/6 - 2/3 = 1/6
2. Which is the smallest

A. 13/16 B. 15/19 C. 17/21 D. 7/8

Answers: Option (B)
3. 617 + 6.017 + 0.617 + 6.0017 = ?

A. 62.96357 B. 62963.57 C. 62.96357 D. 629.6357

Answers: Option (D)
4. Find the value of X 3889 + 12.952 - X = 3854.002

A. 47.95 B. 44.95 C. 43.95 D. 40.95

Answers: Option (A)
5. If 144/0.144 = 14.4/x, then x = ?

A. 0.144 B. 0.0144 C. .00144 D. 1.44

Answers: Option (B)
Relationship
1. If A is the brother of B; B is the sister of C; and C is the father of D, how D is related to A?

A. Brother B. Sister C. Nephew D. Cannot be determined

Answers: Option (D)
Explanation: If D is Male, the answer is Nephew. If D is Female, the answer is Niece. As the sex of D is not known, hence, the relation between D and A cannot be determined. Note: Niece - A daughter of one's brother or sister, or of one's brother-in-law or sister-in-law. Nephew - A son of one's brother or sister, or of one's brother-in-law or sister-in-law.
2. Introducing a boy, a girl said, "He is the son of the daughter of the father of my uncle." How is the boy related to the girl?

A. Brother B. Nephew C. Uncle D. Son-in-law

Answers: Option (A)
Explanation: The father of the boy's uncle → the grandfather of the boy and daughter of the grandfather → sister of the father.
3. Pointing a photograph X said to his friend Y, "She is the only daughter of the father of my mother." How X is related to the person of the photograph?

A. Daughter B. Son C. Nephew D. Cannot be decided

Answers: Option (B)
Explanation: 'The only daughter of the father of X's mother' means mother of X. Hence X is the son of the lady in the photograph.
4. Veena who is the sister-in-law of Ashok is the daughter-in-law of Kalyani. Dheeraj is the father of Sudeep who is the only brother of Ashok. How Kalyani is related to Ashok?

A. Mother-in-law B. Aunt C. Wife D. None of these

Answers: Option (D)
Explanation: Ashok is the only brother of Sudeep and Veena is the sister-in-law of Ashok. Hence Veena is the wife of Sudeep. Kalyani is the mother-in-law of Veena. Kalyani is the mother of Ashok.
5. Pointing to a woman, Abhijit said, "Her granddaughter is the only daughter of my brother." How is the woman related to Abhijit?

A. Sister B. Grandmother C. Mother-in-law D. Mother

Answers: Option (D)
Explanation: Daughter of Abhijit's brother → niece of Abhijit. Thus the granddaughter of the woman is Abhijit's niece. Hence, the woman is the mother of Abhijit.
Relationship between Numbers
1. If M is a number such that M ÷ 5 gives a remainder of 1, then which of the following is the one’s digit of M?

A. 1 B. 6 C. 1 or 6 D. none of these.

Answers: Option (C)
2. A number divisible by 9 is also divisible by:

A. 3 B. 6 C. 11 D. none of these.

Answers: Option (A)
3. If [3X 74] is a number divisible by 9, then the least value of X is:

A. 1 B. 2 C. 3 D. 4

Answers: Option (D)
4. If [1X 2Y 6Z] is a number divisible by 9, then the least value of X + Y + Z is:

A. 0 B. 1 C. 6 D. 9

Answers: Option (A)
5. The number 2 8 2 2 1 is divisible by which of the following:

A. 2 B. 3 C. 6 D. 9

Answers: Option (B)
Fundamental arithmetical operations
1. If V means ‘divided by, – means ‘multiplied by’, V means ‘minus and V means ‘plus’, which of the following will be the value of the expression 16+ 8- 4 + 2 x 4?

A. 16 B. 28 C. 32 D. 44 E. None of these

Answers: Option (B)
2. If + means +, – means x, + means + and x means then 36 x 12 + 4 + 6 + 2 – 3 = ?

A. 2 B. 18 C. 42 D. 6 E. None of these

Answers: Option (C)
3. If A means ‘plus’, B means ‘minus’, C means ‘divided by’ and D means ‘multiplied by’, then 18 A 12 C 6 D 2 B 5 =?

A. 15 B. 25 C. 27 D. 45 E. None of these

Answers: Option (E)
4. If x stands for + stands for +, + stands for + and – stands for x, which one of the following equations is correct?

A. 15 – 5 + 6 x 20 + 10 = 6 B. 8 + 10 – 3 + 5 x 6 = 8 C. 6 x 2 + 3 + 12 – 3 = 15 D. 3 + 7 – 5 x 1 0 + 3 = 10

Answers: Option (B)
5. If x stands for ‘addition’, + stands for ‘subtraction’, + stands for ‘multiplication’ and – stands for ‘division’, then 20 x 8 + 8 – 4 + 2 – ?

A. 80 B. 25 C. 24 D. 5

Answers: Option (C)
Percentages
1. Subtracting 10% from X is the same as multiplying X by what number?

A. 80% B. 90% C. 10% D. 50%

Answers: Option (B)
Explanation: X - (10/100) X = X * ? ? = 90%
2. If the numerator of a fraction is increased by 20% and its denominator is diminished by 25% value of the fraction is 2/15. Find the original fraction.

A. 1/12 B. 1/8 C. 1/6 D. 1/4

Answers: Option (A)
Explanation: X * (120/100) ---------------- = 2/15 Y * (75/100) X/Y = 1/12
3. A and B’s salaries together amount to Rs. 2,000. A spends 95% of his salary and B spends 85% of his. If now their savings are the same, what is A’s salary?

A. Rs.500 B. Rs.750 C. Rs.1250 D. Rs.1500

Answers: Option (D)
Explanation: (5/100) A = (15/100) B A = 3B A + B = 2000 4B = 2000 => B = 500 A = 1500.
4. A salesman’s terms were changed from a flat commission of 5% on all his sales to a fixed salary of Rs.1000 plus 2.5% commission on all sales exceeding Rs. 4,000. If his remuneration as per the new scheme was Rs. 600 more than that by the previous schema, his sales were worth?

A. Rs. 14,000 B. Rs. 12,000 C. Rs. 30,000 D. Rs. 40,000

Answers: Option (B)
Explanation: [1000 + (X-4000) * (2.5/100)] - X * (5/100) = 600 X = 12000.
5. A mixture of 70 litres of wine and water contains 10% water. How much water must be added to make water 12 [latex]\frac {1}{2}[/latex]% of the total mixture?

A. 12 liters B. 10 liters C. 4 liters D. 2 litres

Answers: Option (D)
Explanation: 70 * (10/100) = 7 Wine Water 87 1/2% 12 1/2% 87 1/2% ------- 63 12 1/2% -------? => 9-7=2
Ratio and Proportion
1. If x, y and z are in proportion, then:

A. x : y : : z : x; B. x : y : : y : z; C. x : y : : z : y; D. x : z : : y : z

Answers: Option (B)
2. 7 : 12 is equivalent to:

A. 28 : 40; B. 42 : 71; C. 72 : 42; D. 42 : 72

Answers: Option (D)
3. The length and breadth of a rectangle are in the ratio 3: 1. If the breadth is 7 cm, then the length of the rectangle is:

A. 14 cm; B. 16 cm; C. 18 cm; D. 21 cm

Answers: Option (D)
4. The value of m, if 3, 18, m, 42 are in proportion is:

A. 6; B. 54; C. 7; D. none of these

Answers: Option (C)
5. Length and width of a field are in the ratio 5 : 3. If the width of the field is 42 m then its length is:

A. 100 m; B. 80 m; C. 50 m; D. 70 m.

Answers: Option (D)
Averages
1. The average of first 10 prime numbers is?

A. 10 B. 12.5 C. 12.9 D. 15.5

Answers: Option (C)
Explanation: Sum of 10 prime no. = 129 Average = 129/10 = 12.9
2. The average age of three boys is 15 years and their ages are in proportion 3:5:7. What is the age in years of the youngest boy?

A. 15 B. 9 C. 18 D. 21

Answers: Option (B)
Explanation: 3x + 5x + 7x = 45 x =3 3x = 9
3. The average of 9 observations was 9, that of the 1st of 5 being 10 and that of the last 5 being 8. What was the 5[latex]^{th}[/latex] observation?

A. 9 B. 8 C. 7 D. 6

Answers: Option (A)
Explanation: 1 to 9 = 9 * 9 = 81 1 to 5 = 5 * 10 = 50 5 to 9 = 5 * 8 = 40 5[latex]^{th}[/latex] = 50 + 40 = 90 – 81 = 9.
4. The average of 10 numbers is calculated as 15. It is discovered later on that while calculating the average, one number namely 36 was wrongly read as 26. The correct average is?

A. 12.4 B. 14 C. 16 D. 18.6

Answers: Option (C)
Explanation: 10 * 15 + 36 – 26 = 160/10 = 16.
5. The average of the first five prime numbers greater than 20 is?

A. 31.00 B. 31.01 C. 32.00 D. 32.2

Answers: Option (D)
Explanation: 23 + 29 + 31 + 37 + 41 = 161/5 = 32.2
Interest
1. A certain sum amounts to Rs.1725 in 3 years and Rs.1875 in 5 years. Find the rate % per annum?

A. 3% B. 5% C. 6% D. 4%

Answers: Option (B)
Explanation: 3 --- 1725 5 --- 1875 -------------- 2 --- 150 N = 1 I = 75 R = ? P = 1725 - 225 = 1500 75 = (1500*1*R)/100 R = 5%
2. At what rate percent on simple interest will a sum of money double itself in 30 years?

A. 3 1/3 % B. 3 1/2% C. 4 % D. 4 1/2 %

Answers: Option (A)
Explanation: P = (P*30*R)/100 R = 3 [latex]\frac {1}{3}[/latex]
3. A certain sum of money at simple interest amounted Rs.840 in 10 years at 3% per annum, find the sum?

A. Rs.500 B. Rs.515 C. Rs.525 D. None

Answers: Option (D)
Explanation: 840 = P [1 + (10*3)/100] P = 646.
4. If x is the interest on y and y is the interest on z, the rate and time is the same on both the cases. What is the relation between x, y and z?

A. xyz = 1 B. X[latex]^{2}[/latex] = yz C. Y[latex]^{2}[/latex] = xz D. Z[latex]^{2}[/latex] = xy

Answers: Option (C)
Explanation: X = (Y*NR)/100 Y = (Z*NR)/100 X/Y = NR/100 Y/Z = NR/100 X/Y = Y/Z Y[latex]^{2}[/latex] = XZ
5. Rs.2500 is divided into two parts such that if one part be put out at 5% simple interest and the other at 6%, the yearly annual income may be Rs.140. How much was lent at 5%?

A. Rs.1500 B. Rs.1300 C. Rs.1200 D. Rs.1000

Answers: Option (D)
Explanation: (x*5*1)/100 + [(2500 - x)*6*1]/100 = 140 X = 1000.
Profit and Loss
1. The sale price sarees listed for Rs.400 after successive discount is 10% and 5% is?

A. Rs.357 B. Rs.340 C. Rs.342 D. Rs.338

Answers: Option (C)
Explanation: 400*(90/100)*(95/100) = 342
2. The list price of an article is Rs.65. A customer pays Rs.56.16 for it. He was given two successive discounts, one of them being 10%. The other discount is?

A. 3% B. 4% C. 5% D. 6%

Answers: Option (B)
Explanation: 65*(90/100)*((100-x)/100) = 56.16 x = 4%
3. A single discount equivalent to the discount series of 20%, 10% and 5% is?

A. 25% B. 30% C. 31.6% D. 33.5%

Answers: Option (C)
Explanation: 100*(80/100)*(90/100)*(95/100) = 68.4 100 - 68.4 = 31.6.
4. A trader bought a car at 20% discount on its original price. He sold it at a 40% increase on the price he bought it. What percent of profit did he make on the original price?

A. 10% B. 11% C. 12% D. 15%

Answers: Option (C)
Explanation: Original price = 100 CP = 80 S = 80*(140/100) = 112 100 - 112 = 12%
5. A man sells a horse for Rs.800 and loses something, if he had sold it for Rs.980, his gain would have been double the former loss. Find the cost price of the horse?

A. Rs.900 B. Rs.875 C. Rs.850 D. Rs.860

Answers: Option (D)
Explanation: CP = SP + 1CP = SP - g 800 + x = 980 - 2x 3x = 180 => x = 60 CP = 800 + 60 = 860.
Discount
1. Simran gets a discount of 25% on Rs. 3600 oven. Since she pays cash, she gets additional 2% discount too. How much does she pay?

A. Rs. 2864 B. Rs. 2468 C. Rs. 2548 D. Rs. 2646

Answers: Option (D)
Explanation: 25% discount initially, means price = (100-25)% 0f 3600 = Rs. 2700 2% more discount means 2% of 2700 = Rs. 54 Simran pays = 2700 - 54 = Rs. 2646.
2. If a shopkeeper gives 20% discount and then 10% discount on a pen, which has the marked price of Rs. 500, how much would be the selling price of the pen?

A. Rs. 350 B. Rs. 150 C. Rs. 320 D. Rs. 360

Answers: Option (D)
Explanation: 20% discount means 20% 0f 500 = Rs. 100 is first discount Now price is 500 - 100 = Rs. 40 10% discount means 10% 0f 400 = Rs. 40 Now, selling price = 400 - 40 = Rs. 360.
3. There is a 10% discount on a dozen pairs of trousers marked at Rs. 8000. How many pair of trousers can be bought with Rs. 2400?

A. 7 B. 2 C. 4 D. 8

Answers: Option (C)
Explanation: A dozen pairs mean 12 pairs. Marked price for 12 pairs = Rs. 8000 10% discount, so, final price = 8000 - 10% 0f 8000 = Rs. 7200 Price of 1 pair = [latex]\frac {7200}{12}[/latex] = Rs. 600. How many pair of trousers can be bought in Rs. 2400? Number of pairs of trousers = [latex]\frac {2400}{600}[/latex] = 4 pairs.
4. Blackberry announced a discount of 25% on their trousers. Vivek went to shop. He wanted to save Rs. 400 in discount. How many trousers should he buy to do so, if each trouser costs Rs. 320?

A. 5 B. 4 C. 10 D. 50

Answers: Option (A)
Explanation: Trouser cost = Rs. 320 Discount is 25% of 320 = Rs. 80 For 1 trouser discount is Rs. 80 If vivek wants to save Rs. 400, so he needs to buy [latex]\frac {400}{80}[/latex] = 5 trousers.
5. Sonali could not decide between a discount of 30% or two successive discounts of 25% and 5%, both given on shopping of Rs. 2000. What is the difference between both the discounts?

A. Rs. 15 B. Rs. 25 C. Rs. 100 D. There is no difference

Answers: Option (B)
Explanation: 30% discount on 200 = 30% of 2000 = Rs. 600 25% discount on 2000 = 25% of 2000 = Rs. 500 Remaining amount = 2000 - 500 = Rs.1500 Second discount of 5% = 5% of 1500 = Rs. 75 Total discount = 500 + 75 = 575. So difference in discounts = Rs. 600 - Rs. 575 = Rs. 25.
Tables and Graphs
Study the following table and answer the questions based on it.
Number of Candidates Appeared, Qualified and Selected in a Competitive Examination from Five States
Delhi, H.P, U.P, Punjab and Haryana Over the Years 1994 to 1998

1. For which state the average number of candidates selected over the years is the maximum?

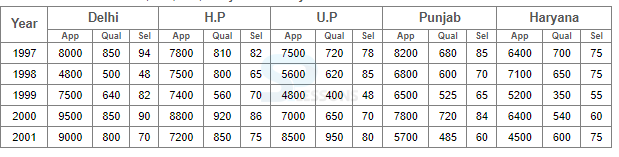
A. Delhi B. H.P C. U.P D. Punjab

Answers: Option (A)
Explanation:
The average number of candidates selected over the given period for various states are:
For Delhi = [latex]\frac {94 + 48 + 82 + 90 + 70}{5}[/latex] =[latex]\frac {384}{5}[/latex]= 76.8.
For H.P. =[latex]\frac {82 + 65 + 70 + 86 + 75}{5}[/latex]=[latex]\frac {378}{5}[/latex]= 75.6.
For U.P. =[latex]\frac {78 + 85 + 48 + 70 + 80}{5}[/latex]=[latex]\frac {361}{5}[/latex]= 72.2.
For Punjab =[latex]\frac {85 + 70 + 65 + 84 + 60}{5}[/latex]=[latex]\frac {364}{5}[/latex]= 72.8.
For Haryana =[latex]\frac {75 + 75 + 55 + 60 + 75}{5}[/latex]=[latex]\frac {340}{5}[/latex]= 68.
Clearly, this average is maximum for Delhi.
2. The percentage of candidates qualified from Punjab over those appeared from Punjab is highest in the year?

A. 1997 B. 1998 C. 1999 D. 2000

Answers: Option (D)
Explanation:
The percentages of candidates qualified from Punjab over those appeared from Punjab during different years are:
For 1997 =([latex]\frac {680}{8200}[/latex]x 100)% = 8.29%.
For 1998 =([latex]\frac {600}{6800}[/latex]x 100)% = 8.82%.
For 1999 =([latex]\frac {525}{6500}[/latex]x 100)% = 8.08%.
For 2000 =([latex]\frac {720}{7800}[/latex]x 100)% = 9.23%.
For 2001 =([latex]\frac {485}{5700}[/latex]x 100)% = 8.51%.
Clearly, this percentage is highest for the year 2000.
3. In the year 1997, which state had the lowest percentage of candidates selected over the candidates appeared?

A. Delhi B. H.P C. U.P D. Punjab

Answers: Option (D)
Explanation:
The percentages of candidates selected over the candidates appeared in 1997, for various states are:
(i) For Delhi = ([latex]\frac {94}{8000}[/latex]x 100) % = 1.175%.
(ii) For H.P. = ([latex]\frac {82}{7800}[/latex]x 100) % = 1.051%.
(iii) For U.P. =([latex]\frac {78}{7500}[/latex]x 100) % = 1.040%.
(iv) For Punjab ([latex]\frac {85}{8200}[/latex]x 100) % = 1.037%.
(v) For Haryana ([latex]\frac {75}{6400}[/latex]x 100) % = 1.172%.
Clearly, this percentage is the lowest for Punjab.
4. The number of candidates selected from Haryana during the period under review is approximately what percent of the number selected from Delhi during this period?

A. 79.5% B. 81% C. 84.5% D. 88.5%

Answers: Option (D)
Explanation: Required percentage = [[latex]\frac {(75 + 75 + 55 + 60 + 75)}{(94 + 48 + 82 + 90 + 70)}[/latex]x 100 ] % =[[latex]\frac {340}{384}[/latex]x 100 ]% = 88.54% ≈ 88.5%
5. The percentage of candidates selected from U.P over those qualified from U.P is highest in the year?

A. 1997 B. 1998 C. 1999 D. 2001

Answers: Option (B)
Explanation:
The percentages of candidates selected from U.P. over those qualified from U.P. during different years are:
For 1997 =([latex]\frac {78}{720}[/latex]x 100 )% = 10.83%.
For 1998 =([latex]\frac {85}{620}[/latex]x 100 )% = 13.71%.
For 1999 =([latex]\frac {48}{400}[/latex]x 100 )% = 12%.
For 2000 =([latex]\frac {70}{650}[/latex]x 100 )% = 10.77%.
For 2001 =([latex]\frac {80}{950}[/latex]x 100 )% = 8.42%.
Clearly, this percentage is highest for the year 1998.
Mensuration
1. The ratio of the length and the breadth of a rectangle is 4 : 3 and the area of the rectangle is 6912 sq cm. Find the ratio of the breadth and the area of the rectangle?

A. 1: 96 B. 1: 48 C. 1: 84 D. 1: 68 E. None of these

Answers: Option (A)
Explanation: Let the length and the breadth of the rectangle be 4x cm and 3x respectively. (4x)(3x) = 6912 12x[latex]^{2}[/latex] = 6912 x[latex]^{2}[/latex] = 576 = 4 * 144 = 2[latex]^{2}[/latex] * 12[latex]^{2}[/latex] (x > 0) => x = 2 * 12 = 24 Ratio of the breadth and the areas = 3x : 12x[latex]^{2}[/latex] = 1 : 4x = 1: 96.
2. The length of a rectangular plot is thrice its breadth. If the area of the rectangular plot is 867 sq m, then what is the breadth of the rectangular plot?

A. 8.5 m B. 17 m C. 34 m D. 51 m E. None of these

Answers: Option (B)
Explanation: Let the breadth of the plot be b m. Length of the plot = 3 b m (3b)(b) = 867 3b[latex]^{2}[/latex] = 867 b[latex]^{2}[/latex] = 289 = 17[latex]^{2}[/latex] (b > 0) b = 17 m.
3. The length of a rectangular floor is more than its breadth by 200%. If Rs. 324 is required to paint the floor at the rate of Rs. 3 per sq m, then what would be the length of the floor?

A. 27 m B. 24 m C. 18 m D. 21 m E. None of these

Answers: Option (C)
Explanation: Let the length and the breadth of the floor be l m and b m respectively. l = b + 200% of b = l + 2b = 3b Area of the floor = 324/3 = 108 sq m l b = 108 i.e., l * l/3 = 108 l[latex]^{2}[/latex] = 324 => l = 18.
4. An order was placed for the supply of a carpet whose breadth was 6 m and length was 1.44 times the breadth. What be the cost of a carpet whose length and breadth are 40% more and 25% more respectively than the first carpet. Given that the ratio of carpet is Rs. 45 per sq m?

A. Rs. 3642.40 B. Rs. 3868.80 C. Rs. 4216.20 D. Rs. 4082.40 E. None of these

Answers: Option (D)
Explanation: Length of the first carpet = (1.44)(6) = 8.64 cm Area of the second carpet = 8.64(1 + 40/100) 6 (1 + 25/100) = 51.84(1.4)(5/4) sq m = (12.96)(7) sq m Cost of the second carpet = (45)(12.96 * 7) = 315 (13 - 0.04) = 4095 - 12.6 = Rs. 4082.40
5. If the sides of a triangle are 26 cm, 24 cm and 10 cm, what is its area?

A. 120 cm[latex]^{2}[/latex] B. 130 cm[latex]^{2}[/latex] C. 312 cm[latex]^{2}[/latex] D. 315 cm[latex]^{2}[/latex] E. None of these

Answers: Option (A)
Explanation: The triangle with sides 26 cm, 24 cm and 10 cm is right-angled, where the hypotenuse is 26 cm. Area of the triangle = 1/2 * 24 * 10 = 120 cm[latex]^{2}[/latex]
Time and Distance
1. If a person walks at 14 km/hr instead of 10 km/hr, he would have walked 20 km more. The actual distance travelled by him is:

A. 50 km B. 56 km C. 70 km D. 80 km

Answers: Option (A)
Explanation: Let the actual distance travelled be x km. Then,[latex]\frac {x}{10}[/latex] = [latex]\frac {x + 20}{14}[/latex] => 14x = 10x + 200 => 4x = 200 => x = 50 km.
2. Excluding stoppages, the speed of a bus is 54 kmph and including stoppages, it is 45 kmph. For how many minutes does the bus stop per hour?

A. 9 B. 10 C. 12 D. 20

Answers: Option (B)
Explanation: Due to stoppages, it covers 9 km less. Time taken to cover 9 km = ([latex]\frac {9}{54}[/latex] x 60) min = 10 min.
3. A man on tour travels first 160 km at 64 km/hr and the next 160 km at 80 km/hr. The average speed for the first 320 km of the tour is:

A. 35.55 km/hr B. 36 km/hr C. 71.11 km/hr D. 71 km/hr

Answers: Option (C)
Explanation: Total time taken = [latex]\frac {160}{64}[/latex]+[latex]\frac {160}{80}[/latex]hrs. = [latex]\frac {9}{2}[/latex]hrs. Average speed = (320 x [latex]\frac {2}{9}[/latex]) km/hr = 71.11 km/hr.
4. In covering a distance of 30 km, Abhay takes 2 hours more than Sameer. If Abhay doubles his speed, then he would take 1 hour less than Sameer. Abhay's speed is:

A. 5 kmph B. 6 kmph C. 6.25 kmph D. 7.5 kmph

Answers: Option (A)
Explanation: Let Abhay's speed be x km/hr. Then, [latex]\frac {30}{x}[/latex] - [latex]\frac {30}{2x}[/latex] = 3 6x = 30 x = 5 km/hr.
5. A farmer travelled a distance of 61 km in 9 hours. He travelled partly on foot @ 4 km/hr and partly on bicycle @ 9 km/hr. The distance travelled on foot is:

A. 14 km B. 15 km C. 16 km D. 17 km

Answers: Option (C)
Explanation: Let the distance travelled on foot be x km. Then, distance travelled on bicycle = (61 -x) km. So, [latex]\frac {x}{4}[/latex] + [latex]\frac {(61 -x)}{9}[/latex] = 9 9x + 4(61 -x) = 9 x 36 5x = 80 x = 16 km.
Time and Work
1. A can do a piece of work in 4 days. B can do it in 5 days. With the assistance of C they completed the work in 2 days. Find in how many days can C alone do it?

A. 10 days B. 20 days C. 5 days D. 4 days

Answers: Option (B)
Explanation: C = 1/2 - 1/4 - 1/5 = 1/20 => 20 days.
2. A can do a piece of work in 30 days. He works at it for 5 days and then B finishes it in 20 days. In what time can A and B together it?

A. 16 2/3 days B. 13 1/3 days C. 17 1/3 days D. 16 1/2 days

Answers: Option (B)
Explanation: 5/30 + 20/x = 1 x = 24 1/30 + 1/24 = 3/40 40/3 = 13 1/3 days.
3. A and B can do a piece of work in 12 days and 16 days respectively. Both work for 3 days and then A goes away. Find how long will B take to complete the remaining work?

A. 15 days B. 12 days C. 10 days D. 9 days

Answers: Option (D)
Explanation: 3/12 + (3 + x)/16 = 1 x = 9 days.
4. A and B can do a piece of work in 3 days, B and C in 4 days, C and A in 6 days. How long will C take to do it?

A. 18 days B. 20 days C. 24 days D. 30 days

Answers: Option (C)
Explanation: 2c = ¼ + 1/6 – 1/3 = 1/12 c = 1/24 => 24 days.
5. A can do a piece of work in 15 days and B in 20 days. They began the work together but 5 days before the completion of the work, A leaves. The work was completed in?

A. 8 days B. 10 days C. 15 days D. 11 3/7 days

Answers: Option (D)
Explanation: (x – 5)/15 + x/20 = 1 x = 11 3/7 days