1. How many such pairs of letters are there in the word SHOULDER each of which has as many letters between them in the word as in the English alphabet?

A. None B. One C. Two D. Three E. More than three

Answer: Option B
2. If it is possible to make only one meaningful English word with the first, the fifth, the seventh and the tenth letters of the word STREAMLINE, using each letter once in each world, which of the following is the third letter of that word? If no such word can be made, give ‘X’ as the answer and if more than one such word can be made, give ‘Y’ as the answer.

A. L B. E C. S D. X E. Y

Answer: Option E Explanation: Meaningful words: SALE, SEAL 1 2 3 4 5 6 7 8 9 10 S T R E A M L I N E
3. Four of the following five are alike in a certain way and so form a group. Which is the one that does not belong to that group?

A. Nitrogen B. Hydrogen C. Methane D. Neon E. Helium

Answer: Option C Explanation: Among these, only Methane is compound gas.
4. In a certain code BREAKING is written BFSCFMHJ, How is MOTHERLY written in that code?

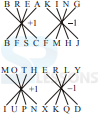
A. IUPNZMSF B. IUPNXKQD C. IUPNFSMZ D. GSNLZMSF E. None of these

Answer: Option B Explanation:
5. Among P, Q, R, S and T Each having a different height, Q is taller than S. T is shorter than P. R is taller than Q but shorter than T. Who among them in the tallest?

A. S B. P C. R D. Data inadequate E. None of these

Answer: Option B Explanation: P > T > R > Q > S i.e., P is the tallest

Read the following information and answer the questions based on it.

P @ Q means P is either greater than or equal to Q P + Q means P is either smaller than or equal to Q P % Q means P is greater than Q P × Q means P is smaller than Q P $ Q means P is neither greater than nor smaller than Q.

Now in each of the following questions assuming the given statement to be true, find which of the two conditions I and II given below them is/are definitely true? Give answer

A. If only conclusion I is true B. If only conclusion II is true C. If either I or II is true D. If neither I or II is true E. If both I and II are true

1. Statements : M @ R, R % T, T $ K Conclusion : (I) K × M, (II) T × M
Answer: Option E Explanation: M [latex]\geq[/latex] R > T = K Conclusion I : K < M (True) Conclusion II : T < M (True) Hence, both conclusions are true.
2. In a certain code language ‘how many are there’ is written as ‘ka na ta da’ and ‘many are welcome here’ is written as ‘na pa ni ka’. How is ‘how’ written in that code language?

A. ta B. da C. ta or da D. Data inadequate E. None of these

Answer: Option C Explanation: how many are there - ka na ta da - (i) many are welcome here - na pi ni ka - (ii) From equations (i) and (ii) many are - na ka how - ta or da
3. If ‘R’ denotes ‘÷’, ‘T’ denotes ‘–’, ‘M’ denotes ‘+’ and ‘W’ denotes ‘×’, then 27 T 15 R 3 W 4 M 6 = ?

A. 7 B. 13 C. -23 D. 1 E. None of these

Answer: Option B Explanation: Given arrangement = 27 T 15 R 3 W 4 M 6 According to question, letters converted into mathematical symbols = 27 – 15 ÷ 3 × 4 + 6 = 27 – 5 × 4 + 6 = 27 – 20 + 6 = 33 – 20 = 13
4. Statements : H % J, B + J, B @ F Conclusion : (I) F $ J, (II) J % F
Answer: Option C Explanation: M > J [latex]\geq[/latex] B [latex]\geq[/latex] F Conclusion I : F = J Conclusion II: J > J Hence, either I or II is true.
5. Statements : D $ M, M % W, W @ R Conclusion : (I) R × D, (II) W + D
Answer: Option A Explanation: D = M > W [latex]\geq[/latex] R Conclusion I : R < D (True) Conclusion II : W [latex]\leq[/latex] D (False) Hence, only conclusion I is true.

1. 172 176 192 256 512 ?

A. 1428 B. 1536 C. 1626 D. 1486 E. None of these

Answer: Option B
Explanation:

2. 180 194 152 222 ? 250

A. 226 B. 126 C. 148 D. 124 E. None of these

Answer: Option D
Explanation:

3. 11 31 59 175 347 ?

A. 1039 B. 987 C. 1123 D. 913 E. None of these

Answer: Option A
Explanation:

4. 45 47 52 62 79 ?

A. 103 B. 96 C. 107 D. 104 E. None of these

Answer: Option C
Explanation:

5. 130 121 103 76 40 ?

A. – 10 B. 5 C. 10 D. – 5 E. None of these

Answer: Option D
Explanation: