Direction to solve(1 to 5): In the world today we make health and end in itself. We have forgotten that health is really means to enable a person to do his work and do it well. a lot of modern medicine and this includes many patients as well as many physicians pays very little attention to health but very much attention to those who imagine that they are ill. Our great concern with health is shown by the medical columns in newspapers. the health articles in popular magazines and the popularity of television programmers and all those books on medicine. We talk about health all the time. Yet for the most part the only result is more people with imaginary illness. The healthy man should not be wasting time talking about health: he should be using health for work. The work does the work that good health possible.
1. Modern medicine is primarily concerned with

A. promotion of good health B. people suffering from imaginary illness C. people suffering from real illness D. increased efficiency in work

2. The passage suggests that

A. health is an end in itself B. health is blessing C. health is only means to an end D. we should not talk about health

3. Talking about the health all time makes people

A. always suffer from imaginary illness B. sometimes suffer from imaginary illness C. rarely suffer from imaginary illness D. often suffer from imaginary illness

4. The passage tells us

A. how medicine should be manufactured B. what healthy man should or should not do C. what television programmes should be about D. how best to imagine illness

5. A healthy man should be concerned with

A. his work which good health makes possible B. looking after his health C. his health which makes work possible D. talking about health

Direction to solve(6 to 10): It is to progress in the human sciences that we must look to undo the evils which have resulted from a knowledge of physical world hastily and superficially acquired by population unconscious of the changes in themselves that the new knowledge has imperative. The road to a happier world than any known in the past lies open before us if atavistic destructive passions can be kept in leash while the necessary adaptations are made. Fears are inevitable in time, but hopes are equally rational and far more likely to bear good fruit. We must learn to think rather less of the dangers to be avoided than of the good that will lie within our grasp if we can believe in it and let it dominate our thoughts. Science, whatever unpleasant consequences it may have by the way, is in its very nature a liberator, a liberator of bondage to physical nature and in time to come, a liberator from the weight of destructive passions. We are on the threshold of utter disaster or unprecedentedly glorious achievement. No previous age has been fraught with problems so momentous; and it is to science that we must look to for a happy future.
6. What does science liberate s from? It is liberate us from

A. fears and destructive passions B. slavery to physical nature and from passions C. bondage to physical nature D. idealistic hopes of glorious future

7. Should human sciences be developed because they will

A. provide more knowledge of the physical word B. make us conscious of the changing world C. make us conscious of the changing in ourselves D. eliminate the destruction caused by a superficial knowledge of the physical world

8. If man's bestial yearning is controlled

A. the future will be tolerable B. the future will be brighter than the present C. the present will be brighter than the future D. the present will become tolerable

9. Fears and hopes according to the author

A. are closely linked with the life of modern man B. can bear fruit C. can yield good results D. are irrational

10. To carve out a bright future man should

A. analyse dangers that lie ahead B. try to avoid dangers C. overcome fear and dangers D. cultivate a positive outlook

Direction to solve(11 to 15): The principal advantage in having a clear cut objective of business is that it does not derail; the enterprise does not stray ...(1)... the direct route that it has set for ...(2)... Enterprises with well defined objectives can conveniently undertake ...(3)... and follow long range development policies. Recognition of objectives ...(4)... the temptation to compromise long range ...(5)... for short term gains and improves coordination in work and consistency in policy.
11. Choose the correct answer

A. from B. on C. along D. towards

12. Choose the correct answer

A. others B. industry C. itself D. government

13. Choose the correct answer

A. production B. research C. audit D. appraisa

14. Choose the correct answer

A. invites B. defers C. shifts D. removes

15. Choose the correct answer

A. objectives B. loses C. interests D. profits

16. Despite of their differences on matters of principles, they all agree on the demand of hike is salary?

A. Despite their B. Despite of the C. Despite for their D. Despite off their E. No correction required

17. The man who has committed such a serious crime must get the mostly severe punishment.

A. be getting the mostly severely B. get the most severe C. have got the most severely D. have been getting the severe most E. No correction required

18. For many centuries in Indian History there was no city so famous like the city of Ujjain.

A. as B. such as C. likewise D. so like E. No correction required

19. We don't know how did the thief made an escape.

A. how the thief did make B. how the thief does make C. how the thief made D. how was the thief made E. No correction required

20. He is a singer of repute, but his yesterday's performance was quite disappointing.

A. performances of yesterday were B. yesterday performance was C. yesterday performance were D. performances about yesterday were E. No correction required

21. Extreme old age when a man behaves like a fool

A. Imbecility B. Senility C. Dotage D. Superannuation

22. That which cannot be corrected

A. Unintelligible B. Indelible C. Illegible D. Incorrigible

23. The study of ancient societies

A. Anthropology B. Archaeology C. History D. Ethnology

24. A person of good understanding knowledge and reasoning power

A. Expert B. Intellectual C. Snob D. Literate

25. A person who insists on something

A. Disciplinarian B. Stickler C. Instantaneous D. Boaster

26. You can play with these kittens quite safely.

A. These kittens can played with quite safely. B. These kittens can play with you quite safely. C. These kittens can be played with you quite safely. D. These kittens can be played with quite safely.

27. A child could not have done this mischief.

A. This mischief could not be done by a child. B. This mischief could not been done by a child. C. This mischief could not have been done by a child. D. This mischief a child could not have been done.

28. James Watt discovered the energy of steam.

A. The energy of steam discovered James Watt. B. The energy of steam was discovered by James Watt. C. James Waht was discovered by the energy of steam. D. James Watt had discovered energy by the steam.

29. She makes cakes every Sunday.

A. Every Sunday cakes made by her. B. Cakes are made by her every Sunday. C. Cakes make her every Sunday. D. Cakes were made by her every Sunday.

30. She spoke to the official on duty.

A. The official on duty was spoken to by her B. The official was spoken to by her on duty. C. She was spoken to by the official on duty. D. She was the official to be spoken to on duty.

Direction to solve(31 to 35): In questions below, each passage consist of six sentences. The first and sixth sentence are given in the beginning. The middle four sentences in each have been removed and jumbled up. These are labelled as P, Q, R and S. Find out the proper order for the four sentences.
31.
S1: In the middle of one side of the square sits the Chairman of the committee, the most important person in the room. P : For a committee is not just a mere collection of individuals. Q : On him rests much of the responsibility for the success or failure of the committee. R : While this is happening we have an opportunity to get the 'feel' of this committee. S : As the meeting opens, he runs briskly through a number of formalities. S6: From the moment its members meet, it begins to have a sort nebulous life of its own. The Proper sequence should be:

A. RSQP B. PQRS C. SQPR D. QSRP

32.
S1: A force of exists between everybody in the universe. P : Normally it is very small but when the one of the bodies is a planet, like earth, the force is considerable. Q : It has been investigated by many scientists including Galileo and Newton. R : Everything on or near the surface of the earth is attracted by the mass of earth. S : This gravitational force depends on the mass of the bodies involved. S6: The greater the mass, the greater is the earth's force of attraction on it. We can call this force of attraction gravity. The Proper sequence should be: The Proper sequence should be:

A. PRQS B. PRSQ C. QSRP D. QSPR

33.
S1: Calcutta unlike other cities kept its trams. P : As a result there horrendous congestion. Q : It was going to be the first in South Asia. R : They run down the center of the road S : To ease in the city decided to build an underground railway line. S6: The foundation stone was laid in 1972. The Proper sequence should be:

A. PRSQ B. PSQR C. SQRP D. RPSQ

34.
S1: For some time in his youth Abraham Lincoln was manager for a shop. P : Then a chance Customer would come. Q : Young Lincoln way of keeping shop was entirely unlike anyone else's R : Lincoln would jump up and attend to his needs and then revert to his reading. S : He used to lie full length on the counter of the shop eagerly reading a book. S6: Never before had Lincoln had so much time for reading as had then. The Proper sequence should be:

A. SRQP B. QSPR C. SQRP D. QPSR

35.
S1: All the land was covered by the ocean. P : The leading god fought the monster, killed it and chopped its body in to two halves. Q : A terrible monster prevented the gods from separating the land from the water. R : The god made the sky out of the upper part of the body and ornamented it with stars. S : The god created the earth from the lower part, grew plants on it and populated it with animals. S6: The god molded the first people out of clay according to his own image and mind. The Proper sequence should be:

A. PQRS B. PQSR C. QPSR D. QPRS

Direction to solve(36 to 40): Rearrange the following five sentences in proper sequence so as to for a meaningful paragraph, then answer the questions given below them.
1. After Examining him, the doctor smiled at him mischievously and took out a syringe. 2. Thinking that he was really sick, his father summoned the family doctor. 3. That day, Mintu wanted to take a day off from school 4. Immediately, Mintu jumped up from his bed and swore the he was fine 5. Therefor; he pretended to be sick and remained in bed.
36. Which sentence should come third in the paragraph?

A. 1 B. 2 C. 3 D. 4 E. 5

37. Which sentence should come last in the paragraph?

A. 1 B. 2 C. 3 D. 4 E. 5

38. Which sentence should come fourth in the paragraph?

A. 1 B. 2 C. 3 D. 4 E. 5

39. Which sentence should come second in the paragraph?

A. 1 B. 2 C. 3 D. 4 E. 5

40. Which sentence should come first in the paragraph?

A. 1 B. 2 C. 3 D. 4 E. 5

Answer & Explanation:
1. Answer: Option B
2. Answer: Option C
3. Answer: Option D
4. Answer: Option B
5. Answer: Option A
6. Answer: Option B
7. Answer: Option D
8. Answer: Option B
9. Answer: Option A
10. Answer: Option D
11. Answer: Option A
12. Answer: Option C
13. Answer: Option A
14. Answer: Option D
15. Answer: Option A
16. Answer: Option A
17. Answer: Option B
18. Answer: Option A
19. Answer: Option C
20. Answer: Option E
21. Answer: Option C
22. Answer: Option D
23. Answer: Option B
24. Answer: Option B
25. Answer: Option B
26. Answer: Option D
27. Answer: Option C
28. Answer: Option B
29. Answer: Option B
30. Answer: Option A
31. Answer: Option D
32. Answer: Option D
33. Answer: Option D
34. Answer: Option B
35. Answer: Option D
36. Answer: Option B
37. Answer: Option D
38. Answer: Option A
39. Answer: Option E
40. Answer: Option C

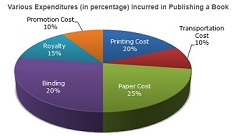
Direction to solve(1 to 5): The following pie-chart shows the percentage distribution of the expenditure incurred in publishing a book. Study the pie-chart and the answer the questions based on it.

1. If for a certain quantity of books, the publisher has to pay Rs. 30,600 as printing cost, then what will be amount of royalty to be paid for these books?

A. Rs. 19,450 B. Rs. 21,200 C. Rs. 22,950 D. Rs. 26,150

2. What is the central angle of the sector corresponding to the expenditure incurred on Royalty?

A. 15° B. 24° C. 54° D. 48°

3. The price of the book is marked 20% above the C.P. If the marked price of the book is Rs. 180, then what is the cost of the paper used in a single copy of the book?

A. Rs. 36 B. Rs. 37.50 C. Rs. 42 D. Rs. 44.25

4. If 5500 copies are published and the transportation cost on them amounts to Rs. 82500, then what should be the selling price of the book so that the publisher can earn a profit of 25%?

A. Rs. 187.50 B. Rs. 191.50 C. Rs. 175 D. Rs. 180

5. Royalty on the book is less than the printing cost by:

A. 5% B. 33% C. 20% D. 25%

Direction to solve(6 to 10): The bar graph given below shows the foreign exchange reserves of a country (in million US $) from 1991 - 1992 to 1998 - 1999.

6. The ratio of the number of years, in which the foreign exchange reserves are above the average reserves, to those in which the reserves are below the average reserves is?

A. 2:6 B. 3:4 C. 3:5 D. 4:4

7. The foreign exchange reserves in 1997-98 was how many times that in 1994-95?

A. 0.7 B. 1.2 C. 1.4 D. 1.5

8. For which year, the percent increase of foreign exchange reserves over the previous year, is the highest?

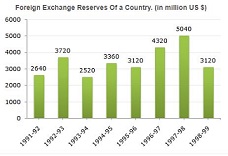
A. 1992-93 B. 1993-94 C. 1994-95 D. 1996-97

9. The foreign exchange reserves in 1996-97 were approximately what percent of the average foreign exchange reserves over the period under review?

A. 95% B. 110% C. 115% D. 125%

10. What was the percentage increase in the foreign exchange reserves in 1997-98 over 1993-94?

A. 100 B. 150 C. 200 D. 620

11. I. [latex]x^{2}[/latex] - x - 42 = 0, II. [latex]y^{2}[/latex] - 17y + 72 = 0 to solve both the equations to find the values of x and y?

A. If x < y B. If x > y C. If x ≤ y D. If x ≥ y E. If x = y or the relationship between x and y cannot be established.

12. I. [latex]x^{2}[/latex] + 9x + 20 = 0, II. [latex]y^{2}[/latex] + 5y + 6 = 0 to solve both the equations to find the values of x and y?

A. If x < y B. If x > y C. If x ≤ y D. If x ≥ y E. If x = y or the relationship between x and y cannot be established.

13. I. [latex]x^{2}[/latex] + 3x - 18 = 0, II. [latex]y^{2}[/latex] + y - 30 = 0 to solve both the equations to find the values of x and y?

A. If x < y B. If x > y C. If x ≤ y D. If x ≥ y E. If x = y or the relationship between x and y cannot be established.

14. I. [latex]x^{2}[/latex] + 11x + 30 = 0, II. [latex]y^{2}[/latex] + 15y + 56 = 0 to solve both the equations to find the values of x and y?

A. If x < y B. If x > y C. If x ≤ y D. If x ≥ y E. If x = y or the relationship between x and y cannot be established.

15. I. 9[latex]a^{2}[/latex] + 18a + 5 = 0, II. 2[latex]b^{2}[/latex] + 13b + 20 = 0 to solve both the equations to find the values of a and b?

A. If a > b B. If a ≥ b C. If a < b D. If a ≤ b E. If a = b or the relationship between a and b cannot be established.

16. Look at this series: 80, 10, 70, 15, 60, ... What number should come next?

A. 20 B. 25 C. 30 D. 50

17. Look at this series: 2, 6, 18, 54, ... What number should come next?

A. 108 B. 148 C. 162 D. 216

18. Look at this series: 5.2, 4.8, 4.4, 4, ... What number should come next?

A. 3 B. 3.3 C. 3.5 D. 3.6

19. Look at this series: 8, 6, 9, 23, 87 , ... What number should come next?

A. 128 B. 226 C. 324 D. 429

20. Look at this series: 1.5, 2.3, 3.1, 3.9, ... What number should come next?

A. 4.2 B. 4.4 C. 4.7 D. 5.1

21. A man has Rs.480 in the denominations of one-rupee notes, five-rupee notes and ten-rupee notes. The number of notes of each denomination is equal. What is the total number of notes that he has ?

A. 45 B. 60 C. 75 D. 90

22. There are two examinations rooms A and B. If 10 students are sent from A to B, then the number of students in each room is the same. If 20 candidates are sent from B to A, then the number of students in A is double the number of students in B. The number of students in room A is:

A. 20 B. 80 C. 100 D. 200

23. If a - b = 3 and [latex]a^{2}[/latex] + [latex]b^{2}[/latex] = 29, find the value of ab.

A. 10 B. 12 C. 15 D. 18

24. In a regular week, there are 5 working days and for each day, the working hours are 8. A man gets Rs. 2.40 per hour for regular work and Rs. 3.20 per hours for overtime. If he earns Rs. 432 in 4 weeks, then how many hours does he work for ?

A. 160 B. 175 C. 180 D. 195

25. A man has some hens and cows. If the number of heads be 48 and the number of feet equals 140, then the number of hens will be:

A. 22 B. 23 C. 24 D. 26

26. Find the highest common factor of 36 and 84.

A. 4 B. 6 C. 12 D. 18

27. On selling 17 balls at Rs. 720, there is a loss equal to the cost price of 5 balls. The cost price of a ball is:

A. Rs. 45 B. Rs. 50 C. Rs. 55 D. Rs. 60

28. A man took loan from a bank at the rate of 12% p.a. simple interest. After 3 years he had to pay Rs. 5400 interest only for the period. The principal amount borrowed by him was:

A. Rs. 2000 B. Rs. 10,000 C. Rs. 15,000 D. Rs. 20,000

29. Find the compound interest on Rs. 10,000 at 20% per annum for 6 months. compounded quarterly.

A. Rs.4353 B. Rs. 1329 C. Rs. 1025 D. Rs. 2649

30. The sum of ages of 5 children born at the intervals of 3 years each is 50 years. What is the age of the youngest child?

A. 4 years B. 8 years C. 10 years D. None of these

31. Sakshi can do a piece of work in 20 days. Tanya is 25% more efficient than Sakshi. The number of days taken by Tanya to do the same piece of work is:

A. 15 B. 16 C. 18 D. 25

32. A farmer traveled a distance of 61 km in 9 hours. He traveled partly on foot @ 4 km/hr and partly on bicycle @ 9 km/hr. The distance traveled on foot is:

A. 14 km B. 15 km C. 16 km D. 17 km

33. Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket drawn has a number which is a multiple of 3 or 5?

A. [latex]\frac{1}{2}[/latex] B. [latex]\frac{2}{5}[/latex] C. [latex]\frac{8}{15}[/latex] D. [latex]\frac{9}{20}[/latex]

34. In how many different ways can the letters of the word 'LEADING' be arranged in such a way that the vowels always come together?

A. 360 B. 480 C. 720 D. 5040 E. None of these

35. The average weight of A, B and C is 45 kg. If the average weight of A and B be 40 kg and that of B and C be 43 kg, then the weight of B is:

A. 17 kg B. 20 kg C. 26 kg D. 31 kg

36. A sum of money is to be distributed among A, B, C, D in the proportion of 5 : 2 : 4 : 3. If C gets Rs. 1000 more than D, what is B's share?

A. Rs. 500 B. Rs. 1500 C. Rs. 2000 D. None of these

37. Aman started a business investing Rs. 70,000. Rakhi joined him after six months with an amount of Rs.. 1,05,000 and Sagar joined them with Rs. 1.4 lakhs after another six months. The amount of profit earned should be distributed in what ratio among Aman, Rakhi and Sagar respectively, 3 years after Aman started the business?

A. 7 : 6 : 10 B. 12 : 15 : 16 C. 42 : 45 : 56 D. Cannot be determined

38. A boat can travel with a speed of 13 km/hr in still water. If the speed of the stream is 4 km/hr, find the time taken by the boat to go 68 km downstream.

A. 2 hours B. 3 hours C. 4 hours D. 5 hours

39. Two trains running in opposite directions cross a man standing on the platform in 27 seconds and 17 seconds respectively and they cross each other in 23 seconds. The ratio of their speeds is:

A. 1 : 3 B. 3 : 2 C. 3 : 4 D. None of these

40. A tank is filled in 5 hours by three pipes A, B and C. The pipe C is twice as fast as B and B is twice as fast as A. How much time will pipe A alone take to fill the tank?

A. 20 hours B. 25 hours C. 35 hours D. Cannot be determined E. None of these

Direction (41-45): Read the following information carefully and answer the questions given below.

41. Find the average of the number of female in all the colleges except college C and E?

A. 672.8 B. 683.5 C. 750 D. 753.5 E. 602.8

42. Find the average difference between the number of male and female students in all the colleges?

A. 312.833 B. 314.60 C. 313 D. 314.50 E. None of these

43. The number of female students in college C is what approx. percent of the number of male students of college A?

A. 70% B. 72% C. 74% D. 76% E. 77%

44. Out of total female in college E, 30% are in Arts department which is 35% of the total students in Arts department. Find out approximately how much percent of male students from E are in Arts department?

A. 20% B. 22% C. 19% D. 23% E. 25%

45. Find the ratio of [latex]\frac{2}{3}^{rfd}[/latex] of college B male students and female students of college F.

A. 29: 11 B. 29: 33 C. 33: 29 D. 29: 22 E. 22: 29

Direction (46-50): Study the following graph carefully to answer the question given below: Given below is the demand and production of 6 brands (in units) of a product in the year 2016.

46. If the demand for brand C product increase by 75% then to meet the demand production should be increased by what percent?

A. 32.65% B. 48.48% C. 57.14% D. 31.25% E. None of these

47. Brand A increase its production to meet its demand. With every 160 unit produced the brand increases its price by 10%. If the earlier price of one product was INR 5000 then find the new price of the product.

A. INR 5500 B. INR 6655 C. INR 7320.5 D. INR 8052.55 E. Cannot be determined

48. The demand for brand D product fell. The new demand is 20% less than its production. Find by what percentage demand fell?

A. 28% B. 30% C. 38.88% D. 72% E. 32%

49. Brand B decreased its price of the product to meet its demand to its production. When the price decreased by 12% the demand increased by 25%. If the ratio between the new price and new demand is 11:20 then find the price of the product before the decrease.

A. INR 2500 B. INR 2300 C. INR 2200 D. INR 2000 E. INR 2800

50. The production of brand E and F took together is approx. what percent of total demand of E and F?

A. 81% B. 21% C. 123% D. 121% E. 23%

Answer: Option
Explanation:
Answer & Explanation:
1. Answer: Option C
Explanation: Let the amount of Royalty to be paid for these books be Rs. r. Then, 20 : 15 = 30600 : r r = Rs.([latex]\frac{30600 x 15}{20}[/latex])= Rs. 22,950
2. Answer: Option C
Explanation: Central angle corresponding to Royalty = (15% of 360)° = [latex]\frac{15}{100}[/latex] * 360 = 54°
3. Answer: Option B
Explanation: Clearly, marked price of the book = 120% of C.P. Also, cost of paper = 25% of C.P Let the cost of paper for a single book be Rs. n. Then, 120 : 25 = 180 : n n = Rs.[latex]\frac{25 * 180}{120}[/latex]= Rs. 37.50
4. Answer: Option A
Explanation: For the publisher to earn a profit of 25%, S.P. = 125% of C.P. Also Transportation Cost = 10% of C.P. Let the S.P. of 5500 books be Rs. x. Then, 10 : 125 = 82500 : x x = Rs. ([latex]\frac{125 x 82500}{10}[/latex])= Rs. 1031250 S.P. of one book = Rs.[latex]\frac{1031250}{5500}[/latex]= Rs. 187.50
5. Answer: Option D
Explanation: Printing Cost of book = 20% of C.P. Royalty on book = 15% of C.P. Difference = (20% of C.P.) - (15% of C.P) = 5% of C.P. Therefore Percentage difference = ([latex]\frac{Difference}{Printing Cost}[/latex]*100)% = ([latex]\frac{5% of C.P.}{Printing Cost}[/latex]*100)% = 25%
6. Answer: Option C
Explanation: Average foreign exchange reserves over the given period = 3480 million US $. The country had reserves above 3480 million US $ during the years 1992-93, 1996-97 and 1997-98, i.e., for 3 years and below 3480 million US $ during the years 1991-92, 1993-94, 1994-95, 1995-56 and 1998-99 i.e., for 5 years. Hence, required ratio = 3 : 5.
7. Answer: Option D
Explanation: Required ratio =[latex]\frac{5040}{3360}[/latex]= 1.5
8. Answer: Option A
Explanation: There is an increase in foreign exchange reserves during the years 1992 - 1993, 1994 - 1995, 1996 - 1997, 1997 - 1998 as compared to previous year (as shown by bar-graph). The percentage increase in reserves during these years compared to previous year are: For 1992 - 1993 =[[latex]\frac{(3720 - 2640)}{2640}[/latex]* 100]% = 40.91%. For 1994 - 1995 =[[latex]\frac{(3360 - 2520)}{2520}[/latex]* 100]% = 33.33% For 1996 - 1997 =[[latex]\frac{(4320 - 3120)}{3120}[/latex]* 100]% = 38.46% For 1997 - 1998 =[[latex]\frac{(5040 - 4320)}{4320}[/latex]* 100]% = 16.67% Clearly, the percentage increase over previous year is highest for 1992 - 1993
9. Answer: Option D
Explanation: Average foreign exchange reserves over the given period = [[latex]\frac{1}{8}[/latex]* (2640 + 3720 + 2520 + 3360 + 3120 + 4320 + 5040 + 3120)]million US $ = 3480 million US $. Foreign exchange reserves in 1996 - 1997 = 4320 million US $. Therefore Required percentage =([latex]\frac{4320}{3480}[/latex]* 100)% = 124.14% ~= 125%
10. Answer: Option A
Explanation: Foreign exchange reserves in 1997 - 1998 = 5040 million US $. Foreign exchange reserves in 1993 - 1994 = 2520 million US $. Therefore Increase = (5040 - 2520) = 2520 US $. Therefore Percentage Increase =([latex]\frac{2520}{2520}[/latex]* 100)% = 100%
11. Answer: Option A
Explanation: I. [latex]x^{2}[/latex] - 7x + 6x - 42 = 0 (x - 7)(x + 6) = 0 => x = 7, -6 II. [latex]y^{2}[/latex] - 8y - 9y + 72 = 0 (y - 8)(y - 9) = 0 => y = 8, 9 = x < y
12. Answer: Option A
Explanation: I. [latex]x^{2}[/latex] + 4x + 5x + 20 = 0 (x + 4)(x + 5) = 0 => x = -4, -5 II. [latex]y^{2}[/latex] + 3y + 2y + 6 = 0 (y + 3)(y + 2) = 0 => y = -3, -2 = x < y.
13. Answer: Option E
Explanation: I. [latex]x^{2}[/latex] + 6x - 3x - 18 = 0 (x + 6)(x - 3) = 0 => x = -6, 3 II. [latex]y^{2}[/latex] + 6y - 5y - 30 = 0 (y + 6)(y - 5) = 0 => y = -6, 5 No relationship can be established between x and y.
14. Answer: Option B
Explanation: I. [latex]x^{2}[/latex] + 6x + 5x + 30 = 0 (x + 6)(x + 5) = 0 => x = -6, -5 II. [latex]y^{2}[/latex] + 8y + 7y + 56 = 0 (y + 8)(y + 7) = 0 => y = -8, -7 = x > y
15. Answer: Option A
Explanation: I. 9[latex]a^{2}[/latex] + 3a + 15a + 5 = 0 (3a + 5)(3a + 1) = 0 => a = -[latex]\frac{5}{3}[/latex], -[latex]\frac{1}{3}[/latex] II. 2[latex]b^{2}[/latex] + 8b + 5b + 20 = 0 (2b + 5)(b + 4) = 0 => b = -[latex]\frac{5}{2}[/latex], -4 a is always more than b. = a > b.
16. Answer: Option A
Explanation: This is an alternating addition and subtraction series. In the first pattern, 10 is subtracted from each number to arrive at the next. In the second, 5 is added to each number to arrive at the next.
17. Answer: Option C
Explanation: This is a simple multiplication series. Each number is 3 times more than the previous number.
18. Answer: Option D
Explanation: In this simple subtraction series, each number decreases by 0.4.
19. Answer: Option D
Explanation: 8 * 1 - 2 = 6 6 * 2 - 3 = 9 9 * 3 - 4 = 23 23 * 4 - 5 = 87 87 * 5 - 6 = 429 ...
20. Answer: Option C
Explanation: In this simple addition series, each number increases by 0.8.
21. Answer: Option D
Explanation: Let number of notes of each denomination be x. Then x + 5x + 10x = 480 16x = 480 x = 30. Hence, total number of notes = 3x = 90.
22. Answer: Option C
Explanation: Let the number of students in rooms A and B be x and y respectively. Then, x - 10 = y + 10 x - y = 20 .... (i) and x + 20 = 2(y - 20) x - 2y = -60 .... (ii) Solving (i) and (ii) we get: x = 100 , y = 80. The required answer A = 100.
23. Answer: Option C
Explanation: 2ab = ([latex]a^{2}[/latex] + [latex]b^{2}[/latex]) - (a - b)2 = 29 - 9 = 20 ab = 10.
24. Answer: Option B
Explanation: Suppose the man works overtime for x hours. Now, working hours in 4 weeks = (5 x 8 x 4) = 160. 160 x 2.40 + x x 3.20 = 432 3.20x = 432 - 384 = 48 x = 15. Hence, total hours of work = (160 + 15) = 175.
25. Answer: Option D
Explanation: Let the number of hens be x and the number of cows be y. Then, x + y = 48 .... (i) and 2x + 4y = 140 x + 2y = 70 .... (ii) Solving (i) and (ii) we get: x = 26, y = 22. The required answer = 26.
26. Answer: Option C
Explanation: 36 = [latex]2^{2}[/latex] x [latex]3^{2}[/latex] 84 = [latex]2^{2}[/latex] x 3 x 7 H.C.F. = [latex]2^{2}[/latex] x 3 = 12.
27. Answer: Option D
Explanation: (C.P. of 17 balls) - (S.P. of 17 balls) = (C.P. of 5 balls) C.P. of 12 balls = S.P. of 17 balls = Rs.720. C.P. of 1 ball = Rs.([latex]\frac{720}{12}[/latex])= Rs. 60
28. Answer: Option C
Explanation: Principal = Rs.([latex]\frac{100 x 5400}{12*3}[/latex])= Rs. 15000
29. Answer: Option C
Explanation: P = 10000, T = 6 months, R = [latex]\frac{20}{4}[/latex] = 5%(rate of interest apply quarterly) By the net% effect we would calculate the effective compound rate of interest for 6 months = 10.25% (Refer to sub-details) CI = 10.25% of 10000 CI =[latex]\frac{10.25 × 10000}{100}[/latex] CI = 1025.
30. Answer: Option A
Explanation: Let the ages of children be x, (x + 3), (x + 6), (x + 9) and (x + 12) years. Then, x + (x + 3) + (x + 6) + (x + 9) + (x + 12) = 50 5x = 20 x = 4. Age of the youngest child = x = 4 years.
31. Answer: Option B
Explanation: Ratio of times taken by Sakshi and Tanya = 125 : 100 = 5 : 4. Suppose Tanya takes x days to do the work. 5 : 4 :: 20 : x x =([latex]\frac{4*20}{5}[/latex]) x = 16 days. Hence, Tanya takes 16 days to complete the work.
32. Answer: Option C
Explanation: Let the distance travelled on foot be x km. Then, distance travelled on bicycle = (61 -x) km. So,[latex]\frac{x}{4}[/latex]+[latex]\frac{(61 -x)}{9}[/latex]= 9 9x + 4(61 -x) = 9 x 36 5x = 80 x = 16 km.
33. Answer: Option D
Explanation: Here, S = {1, 2, 3, 4, ...., 19, 20}. Let E = event of getting a multiple of 3 or 5 = {3, 6 , 9, 12, 15, 18, 5, 10, 20}. P(E) = [latex]\frac{n(E)}{n(S)}[/latex]= [latex]\frac{9}{20}[/latex]
34. Answer: Option C
Explanation: The word 'LEADING' has 7 different letters. When the vowels EAI are always together, they can be supposed to form one letter. Then, we have to arrange the letters LNDG (EAI). Now, 5 (4 + 1 = 5) letters can be arranged in 5! = 120 ways. The vowels (EAI) can be arranged among themselves in 3! = 6 ways. Required number of ways = (120 x 6) = 720.
35. Answer: Option D
Explanation: Let A, B, C represent their respective weights. Then, we have: A + B + C = (45 x 3) = 135 .... (i) A + B = (40 x 2) = 80 .... (ii) B + C = (43 x 2) = 86 ....(iii) Adding (ii) and (iii), we get: A + 2B + C = 166 .... (iv) Subtracting (i) from (iv), we get : B = 31. B's weight = 31 kg.
36. Answer: Option C
Explanation: Let the shares of A, B, C and D be Rs. 5x, Rs. 2x, Rs. 4x and Rs. 3x respectively. Then, 4x - 3x = 1000 x = 1000. B's share = Rs. 2x = Rs. (2 * 1000) = Rs. 2000.
37. Answer: Option B
Explanation: Aman : Rakhi : Sagar = (70,000 x 36) : (1,05,000 x 30) : (1,40,000 x 24) = 12 : 15 : 16.
38. Answer: Option C
Explanation: Speed downstream = (13 + 4) km/hr = 17 km/hr. Time taken to travel 68 km downstream =([latex]\frac{68}{17}[/latex])hrs = 4 hrs
39. Answer: Option B
Explanation: Let the speeds of the two trains be x m/sec and y m/sec respectively. Then, length of the first train = 27x metres, and length of the second train = 17y metres. [latex]\frac{27x + 17y}{x+ y}[/latex]= 23 27x + 17y = 23x + 23y 4x = 6y [latex]\frac{x}{y}[/latex]= [latex]\frac{3}{2}[/latex]
40. Answer: Option C
Explanation: Suppose pipe A alone takes x hours to fill the tank. Then, pipes B and C will take[latex]\frac{x}{2}[/latex] and [latex]\frac{x}{4}[/latex]hours respectively to fill the tank. [latex]\frac{1}{x}[/latex]+[latex]\frac{2}{x}[/latex]+[latex]\frac{4}{x}[/latex]=[latex]\frac{1}{5}[/latex] x = 35 hrs
41. Answer: Option D
Explanation: Total number of students in college A = 1850 54% of the total students are male ⇒ 46% of the total students are female ∴ Number of female students in college A = 46% of 1850 ⇒ Number of female students in college A = 851 Total number of students in college B = 1550 66% of the total students are male ⇒ 34% of the total students are female ∴ Number of female students in college B = 34% of 1550 ⇒Number of female students in college B = 527 Total number of students in college D = 1675 56% of the total students are male ⇒ 44% of the total students are female ∴ Number of female students in college D = 44% of 1675 ⇒ Number of female students in college D = 737 Total number of students in college F = 1450 38% of the total students are male ⇒ 62% of the total students are female ∴ Number of female students in college F = 62% of 1450 ⇒ Number of female students in college F = 899 Now, required average = [latex]\frac{851 + 527 + 737 + 899}{4}[/latex] = [latex]\frac{3014}{4}[/latex] = 753.5
42. Answer: Option A
Explanation: Total number of students in college A = 1850 54% of the total students are male ⇒ 46% of the total students are female ∴8% difference between male and female students ⇒ Difference between male and female students in college A = 8% of 1850 ⇒ Difference between male and female students in college A = 148 Total number of students in college B = 1550 66% of the total students are male ⇒ 34% of the total students are female ∴32% difference between male and female students ⇒ Difference between male and female students in college B = 32% of 1550 ⇒Difference between male and female students in college B = 496 Total number of students in college C = 1340 45% of the total students are male ⇒ 55% of the total students are female ∴10% difference between male and female students ⇒ Difference between male and female students in college C = 10% of 1340 ⇒ Difference between male and female students in college C = 134 Total number of students in college D = 1675 56% of the total students are male ⇒ 44% of the total students are female ∴12% difference between male and female students ⇒ Difference between male and female students in college D = 12% of 1675 ⇒ Difference between male and female students in college D = 201 Total number of students in college E = 1250 72% of the total students are male ⇒ 28% of the total students are female ∴44% difference between male and female students ⇒ Difference between male and female students in college E = 44% of 1250 ⇒ Difference between male and female students in college E = 550 Total number of students in college F = 1450 38% of the total students are male ⇒ 62% of the total students are female ∴ 24% difference between male and female students ⇒ Difference between male and female students in college F = 24% of 1450 ⇒ Difference between male and female students in college F = 348 Now, required average = [latex]\frac{148 + 496 + 134 + 201 + 550 + 348}{6}[/latex] = [latex]\frac{1877}{6}[/latex] = 312.8
43. Answer: Option C
Explanation: Total number of students in college C = 1340 45% of the total students are male ⇒ 55% of the total students are female ∴ Number of female students in the college C = 55% of 1340 ⇒ Number of female students in the college C = 737 Total number of students in college A = 1850 54% of the total students are male ∴ Number of male students in the college A = 54% of 1850 ⇒ Number of male students in the college A = 999 Now, required percentage = [latex]\frac{737}{999}[/latex] × 100 Hence, the number of female students in college C is approx. 74% of number of male students of college A
44. Answer: Option B
Explanation: Total number of students in college E = 1250 72% of the total students are male ⇒ 28% of the total students are female ∴ Number of female students in college E = 28% of 1250 ⇒ Number of female students in college E = 350 Out of 350 students, 30% are in Arts department ⇒ Number of female students in Arts department = 30% of 350 ⇒ Number of female students in Arts department = 105 105 female students is 35% of total students in Arts department Let the total number of students in Arts department be x ⇒ Number of female students in Arts department = 35% of x ⇒ [latex]\frac{7x}{20}[/latex] = 105 ⇒ x = 300 ∴Number of male students in arts department = 300 – 105 = 195 Number of male students in college E = 72% of 1250 ⇒Number of male students in college E = 900 Now, required percentage = [latex]\frac{195}{900}[/latex] × 100= 22%
45. Answer: Option E
Explanation: Total number of students in college B = 1550 66% of the total students are male ∴ Number of male students in college B = 66% of 1550 ⇒ Number of male students in college B = 1023 ∴ [latex]\frac{2}{3}^{rd}[/latex] of male students of college B = 682 Total number of students in college F = 1450 38% of the total students are male ⇒ 62% of the total students are female ∴ Number of female students in college F = 62% of 1450 ⇒ Number of male students in college F = 899 Now, required ratio =[latex]\frac{682}{899}[/latex] = [latex]\frac{22}{29}[/latex] Hence, the ratio of [latex]\frac{2}{3}^{rd}[/latex] of college B male students and female students of college F is 22: 29
46. Answer: Option B
Explanation: Demand for brand C product = 2800 units Demand for brand C product increase by 75% ⇒ New demand of brand C product = 175% of 2800 units ⇒ New demand of brand C product = 4900 units Production of brand C product = 3300 units To meet the demand the brand C should raise the production of product to 4900 units ∴ 1600 more units should be produced. ⇒ required percentage = [latex]\frac{1600}{3300}[/latex] Hence, to meet the demand the brand C should raise the production by 48.48%.
47. Answer: Option D
Explanation: Demand for brand A product = 2200 units Production of brand A product = 1400 units Difference between demand and production of brand A product = 800 units The company has to raise its production t0 2200 to meet its demand for that it has to produce 800 units more. With every 160 unit produced the brand increases its price by 10%. ⇒ Number of times the brand increase its price by 10% = [latex]\frac{800}{160}[/latex] = 5 Earlier price of one product was INR 5000 ⇒ New price of the product = 5000 × [latex]\frac{110}{100}[/latex] ×[latex]\frac{110}{100}[/latex] × [latex]\frac{110}{100}[/latex] × [latex]\frac{110}{100}[/latex] ×[latex]\frac{110}{100}[/latex] Hence, the new price of the product is INR 8052.55
48. Answer: Option A
Explanation: Demand of brand D product = 5000 units Production of brand D product = 4500 units The new demand is 20% less than its production New demand for brand D product = 80% of 4500 units ⇒New demand of brand D product = 3600 units ∴Difference in earlier demand and new demand = 5000 – 3600 = 1400 ⇒Demand fell by 1400 units Now, required percentage =[latex]\frac{1400}{5000}[/latex] × 100 = 28% Hence, the demand for brand D product fell by 28%.
49. Answer: Option A
Explanation: Let the price of the product be INR x The brand B decreased its price by 12% which led to increasing in demand by 25% ⇒ New price of the product = 88% of x Demand for the brand B product = 3200 units ⇒ New demand of the brand B product = 125% of 3200 ⇒ New demand of the brand B product = 4000 units The ratio between the new price and new demand is 11 : 20 ⇒ [latex]\frac{88x}{100 }[/latex] = [latex]\frac{11}{20}[/latex] × 4000 ⇒ x = 2500 Hence, original price of the brand B product is INR 2500
50. Answer: Option C
Explanation: Production of brand E product = 3500 units Production of brand F product = 4400 units Total production of brand E and F = 7900 units Demand of brand E product = INR 2800 units Demand of brand F product = INR 3600 units Total demand of brand E and F = 6400 units Now, required percentage = [latex]\frac{7900}{6400}[/latex] × 100 ≈123%

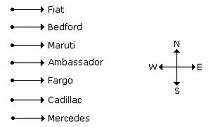
Direction to solve(1 to 5): In an Exhibition seven cars of different companies - Cadillac, Ambassador, Fiat, Maruti, Mercedes, Bedford and Fargo are standing facing to east in the following order :
1. Cadillac is next to right of Fargo. 2. Fargo is fourth to the right of Fiat. 3. Maruti car is between Ambassador and Bedford. 4. Fiat which is third to the left of Ambassador, is at one end.
1. Which of the cars are on both the sides of cadillac car ?

A. Ambassador and Maruti B. Maruti and Fiat C. Fargo and Mercedes D. Ambassador and Fargo

2. Which of the following statement is correct ?

A. Maruti is next left of Ambassador. B. Bedford is next left of Fiat. C. Bedford is at one end. D. Fiat is next second to the right of Maruti.

3. Which one of the following statements is correct ?

A. Fargo car is in between Ambassador and Fiat. B. Cadillac is next left to Mercedes car. C. Fargo is next right of Cadillac. D. Maruti is fourth right of Mercedes.

4. Which of the following groups of cars is to the right of Ambassador ?

A. Cadillac, Fargo and Maruti B. Mercedes, Cadillac and Fargo C. Maruti, Bedford and Fiat D. Bedford, Cadillac and Fargo

5. Which one of the following is the correct position of Mercedes ?

A. Next to the left of Cadillac B. Next to the left of Bedford C. Between Bedford and Fargo D. Fourth to the right of Maruti.

Direction to solve(6 to 9):Each of the following questions is based on the following information:
1. Six flats on a floor in two rows facing North and South are allotted to P, Q, R, S, T and U. 2. Q gets a North facing flat and is not next to S. 3. S and U get diagonally opposite flats. 4. R next to U, gets a south facing flat and T gets North facing flat.
6. If the flats of P and T are interchanged then whose flat will be next to that of U?

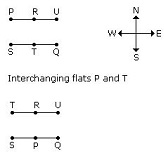
A. P B. Q C. R D. T

7. Which of the following combination get south facing flats?

A. QTS B. UPT C. URP D. Data is inadequate

8. The flats of which of the other pair than SU, is diagonally opposite to each other?

A. QP B. QR C. PT D. TS

9. Whose flat is between Q and S?

A. T B. U C. R D. P

Direction to solve(10 to 13): There are seven members in a family. J is the mother of K and mother in law of E. C is the daughter in law of N. E is the son of C who is married with F. G is spouse of E. There are only two married couple in the family.
10. How is G related with J?

A. Daughter B. Son in law C. daughter in law D. Wife E. Husband

11. How is K related with E?

A. aunt B. Sister C. brother D. CND E. None of these

12. How many male members are there in the family?

A. two B. three C. four D. five E. CND

13. How is F related with G?

A. sister in law B. wife C. mother in law D. brother in law E. none of these

14. In a certain code language, QUEUE is written as Q 22, and CHURCH is written as 1UR1. Which of the following would be most appropriate code for BANANA in that language?

A. B5A5 B. 5N5A C. B55A D. BA5A5A E. B5A5A

15. In a certain code, GIGANTIC is written as GIGTANCI. How is MIRACLES written in that code?

A. MIRLCAES B. MIRLACSE C. RIMCALSE D. RIMLCAES E. RIMSCASE

16. In a certain code, GOODNESS is coded as HNPCODTR. How is GREATNESS coded in that code?

A. HQFZUODTR B. HQFZUMFRT C. HQFZSMFRT D. FSDBSODTR E. HQFZUFRTM

17. If PORTER is written as QNSSFQ, then BRIGHT would be coded as

A. CQJFIS B. CNJHIS C. CQJFGS D. CNJHIU E. None of these

Direction to solve(18 to 20): In each of the questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read both the statements and Give an answer
A. If the data in statement I alone are sufficient to answer the question, while the data in statement II alone are not sufficient to answer the question B. If the data in statement II alone are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question C. If the data either in statement I alone or in statement II alone are sufficient to answer the question D. If the data given in both statements I and II together are not sufficient to answer the question and E. If the data in both statements I and II together are necessary to answer the question.
18. Question: In which year was Rahul born ? Statements: I. Rahul at present is 25 years younger to his mother. II. Rahul's brother, who was born in 1964, is 35 years younger to his mother.

A. I alone is sufficient while II alone is not sufficient B. II alone is sufficient while I alone is not sufficient C. Either I or II is sufficient D. Neither I nor II is sufficient E. Both I and II are sufficient

19. Question: What will be the total weight of 10 poles, each of the same weight ? Statements: I. One-fourth of the weight of each pole is 5 kg. II. The total weight of three poles is 20 kilograms more than the total weight of two poles.

A. I alone is sufficient while II alone is not sufficient B. II alone is sufficient while I alone is not sufficient C. Either I or II is sufficient D. Neither I nor II is sufficient E. Both I and II are sufficient

20. Question: How many children does M have ? Statements: I. H is the only daughter of X who is wife of M. II. K and J are brothers of M.

A. I alone is sufficient while II alone is not sufficient B. II alone is sufficient while I alone is not sufficient C. Either I or II is sufficient D. Neither I nor II is sufficient E. Both I and II are sufficient

Direction to solve(21 to 25): In each question below is given a statement followed by three assumptions numbered I, II and III. You have to consider the statement and the following assumptions, decide which of the assumptions is implicit in the statement and choose your answer accordingly.
21. Statement: In order to reduce the gap between income and expenditure, the company has decided to increase the price of its product from next month. Assumptions: I. The rate will remain more or less same after the increase. II. The expenditure will more or less remain the same in near future. III. The rival companies will also increase the price of the similar product.

A. Only I and II are implicit B. Only II and III are implicit C. Only III is implicit D. All are implicit E. None of these

22. Statement: 'Several labour and industrial courts in this State have no proper premises. Vacancies of judges and stenos are kept pending.' - A statement of a retired judge of State X. Assumptions: I. Adequate number of staff and judges helps in the smooth functioning of the industrial and labour courts. II. The State is not bothered about the condition of the labour and industrial courts. III. Physical facilities of an office help in increasing the efficiency of its employees.

A. Only I and III are implicit B. Only II is implicit C. Only II and III are implicit D. All I, II and III are implicit E. None of these

23. Statement: "A rare opportunity to be a professional while you are at home." - An advertisement for computer literate housewives by a computer company. Assumptions: I. Some housewives simultaneously desire to become professional. II. The computer industry is growing at a fast pace. III. It is possible to be a professional as well as a housewife.

A. Only I and II are implicit B. Only II and III are implicit C. Only I and III are implicit D. Only II is implicit E. None of these

24. Statement: Pramod decided to get the railway reservation in May, for the journey he wants to make in July, to Madras. Assumptions: I. The railways issues reservations two months in advance. II. There are more than one trains to Madras. III. There will be vacancy in the desired class.

A. Only I is implicit B. Only II and III are implicit C. Only I and III are implicit D. All are implicit E. None of these

25. Statement: "To make the company commercially viable, there is an urgent need to prune the staff strength and borrow money from the financial institutions." - Opinion of a consultant. Assumptions: I. The financial institutions lend money for such proposals. II. The product of the company has a potential market. III. The employees of the company are inefficient.

A. None is implicit B. All are implicit C. Only I and II are implicit D. Only II and III are implicit E. Only I and III are implicit

Direction (26-30): Study the following information carefully and answer the question based on it. 8 persons A, B, C, D, E, F, G and H have their birthdays on 14th and 21st of four different months, January, March, April and June not necessarily in the same order. A has birthday on even date and a month which having 31 days. Number of persons between C and F is same as the number of persons between B and H. H’s birthday is neither on even number date nor in a month which having 31 days. B is not born after H. C is born before F and B, who is not born in January. D is not born in June. F was born on even number date. D’s birthday is on odd number date and a month which having 31 days. B and H were not born in the same month. E was born after F. D is born before G.
26. How many persons born after F?

A. 1 B. 2 C. 3 D. 4 E. 5

27. Who among the following is not born in the month having 30 days?

A. F B. D C. B D. H E. E

28. Who among the following does not belongs to the group?

A. A B. D C. G D. B E. H

29. How many persons have birthday between D and E?

A. 1 B. 2 C. 3 D. 4 E. 5

30. Who among the following in not born before F?

A. A B. D C. C D. H E. G

Direction (31-35): Study the following information carefully and answer the questions given below:
Eight persons P, Q, R, S, T, U, V and W are sitting in a straight line and facing north direction. Their ages are, 12, 14, 18, 26, 29, 35 ,42 and 67. The one who is 12 years old is 4 th to the left of the eldest person, who is sitting at the end. The sum of the ages of S and Q is equal to P. S is not the youngest person. S and W are neighbours of Q. R’s age is not an even number and he is older than W and younger than U. Only 3 persons are sitting between S and U. Only 2 persons are sitting between Q and T, who is 29 years old. P is not the neighbour of U. R is not sitting to the left of Q.
31. Who among the following sits at the end?

A. T B. P C. Q D. S E. W

32. Who among the following sits third to the left of W?

A. S B. The one who is 12 years old C. The one who is 26 years old D. T E. U

33. Which of the following pair is neighbour of U?

A. R and W B. S and P C. W and V D. R and V E. Q and R

34. Who among the following is 14 years old?

A. P B. Q C. R D. U E. S

35. How many persons are younger than W?

A. 1 B. 2 C. 3 D. 4 E. None

Direction (36-38): Study the following information carefully and answer the questions given below:
Each of the six students got different marks in an exam. D got less marks than only B. E got more marks than only two students. A didn’t get less marks than E. C did not get least marks. The one who got second lowest, got 160 marks. A got 205 marks. 83. The one
36. who got maximum marks, got 100 marks more than C. Which of the following mark is got by one who got maximum marks?

A. 225 B. 270 C. 260 D. 300 E. None of these

37. Which of the following is true with respect to F as per the given information?

A. The possible marks, got by F is 165 B. F got minimum marks. C. Only two students got more marks than F D. F definitely got more marks than C E. None of these

38. Which of the following may be the possible number of marks which E got?

A. 210 B. 140 C. 185 D. 159 E. None of these

Direction (39-43): Study the following information carefully and answer the question given below:
There are eight persons A, B, C, D, E, F, G and H. They are born in the month (Same for each person) of different years i.e. 1976, 1980, 1982, 1990, 1991, 1995, 2000 and 2005. There ages are considered as on the same month of 2017. B is born in odd number year but he is not the youngest. E is 37 years old now. C was born in 1990. G is at least 9 years older than B. D is younger than B and born in odd number year. A is 18 years younger than G. F is older than D but not the older person. Not more than 2 persons are younger than F.
39. Who among the following is youngest person?

A. A B. C C. D D. B E. G

40. How many persons are older than C?

A. 2 B. 3 C. 1 D. None E. more than 3

41. What is the difference of age between F and E?

A. 15 years B. 10 years C. 30 years D. 4 years E. 12 years

42. If all the persons are arranged according to their names according to alphabet series from youngest to oldest then how many of them position will remain unchanged?

A. 0 B. 1 C. 2 D. 3 E. 4

43. Who among the following is born in 1982?

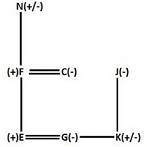
A. D B. G C. A D. C E. H

Directions (44-45): Study the following information carefully and answer the questions given below:
44. Rahul starts running from point A and runs 15 km towards south. He takes a left turn and runs 20 km. Now he runs 9 km after taking a right turn. He finally takes a right turn and runs 20 km and stops at point B. 99. How far is point B with respect to point A?

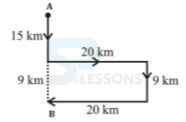
A. 24 km B. 40 km C. 45 km D. 29 km E. 49 km

45. Towards which directions was Rahul moving before he stopped at point B?

A. North B. East C. West D. South E. North-West

Directions (46-48): In these questions, relationship between different elements is shown in the statements. The statements are followed by two conclusions. Find the conclusion which is definitely true.

A. If only Conclusion I is true. B. If only Conclusion II is true. C. If either Conclusion I or II is true. D. If neither Conclusion I nor II is true. E. If both Conclusions I and II are true.

46. Statements: A > B = C < D > F
Conclusions: I. F > D II. II. B > D
47. Statements: A = B < C > D , A > E , D > F
Conclusions: I. F > B II. B > E
48. Statements: A = B > D < E > C < F
Conclusions: I. E > A II. F > D
Directions (49-50): Study the following information carefully and answer the questions given below:
* D is the mother of E, who is the sister of F. * A is the father of C. B is wife of A. * F is son of C.
49. How is E related to A?

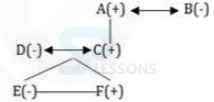
A. Son B. Grandson C. Granddaughter D. Daughter E. None of these

50. How is B related to D?

A. Mother-in-law B. Sister C. Mother D. Can’t be determined E. None of these

Answer & Explanation:
1. Answer: Option C
Explanation: Fargo and Mercedes are on both the sides of cadillac car.
2. Answer: Option A
Explanation: Maruti is next left of Ambassador.
3. Answer: Option B
Explanation: Cadillac is next left to Mercedes car
4. Answer: Option B
Explanation: Cadillac and Fargo cars are to the right of Ambassador.
5. Answer: Option D
Explanation: The correct position of Mercedes is fourth to the right of Maruti.
6. Answer: Option C
Explanation: Hence flat R will be next to U.
7. Answer: Option C
Explanation: URP flat combination get south facing flats.
8. Answer: Option A
Explanation: QP is diagonally opposite to each other.
9. Answer: Option A
Explanation: flat T is between Q and S.
10. Answer: Option A
Explanation:
11. Answer: Option D
12. Answer: Option E
13. Answer: Option E
14. Answer: Option C
Explanation: Similar pairs of letters have been given the same numeric in each word. As a result pair UE in word QUEUE has been coded 2, pair CH has been coded 1 and likewise the pair AN has been coded 5. Hence, the word BANANA would be coded as B55A.
15. Answer: Option B
Explanation: First three letter of the word are kept as they are sixth letter comes at fourth place shifting fourth and fifth letters to fifth and sixth places, respectively and the last two letters are exchanged.
16. Answer: Option B
Explanation: Letters at odd places in the coded word are one letter ahead of the letters in the basic word, and letters at even places are one letter behind of the letters in the basic word as their positions in the alphabet.
17. Answer: Option A
Explanation: Letters at the odd places in the coded word are one letter ahead of the respective letters of the basic word, and letters at the even places in the coded word are one letter back of the respective letters as their positions in the alphabet.
18. Answer: Option E
Explanation: From both I and II, we find that Rahul is (35 - 25) = 10 years older than his brother, who was born in 1964. So, Rahul was born in 1954.
19. Answer: Option C
Explanation: From I, we conclude that weight of each pole = (4 x 5) kg = 20 kg. So, total weight of 10 poles = (20 x 10) kg = 200 kg. From II, we conclude that: Weight of each pole = (weight of 3 poles) - (weight of 2 poles) = 20 kg. So, total weight of 10 pojes = (20 x 10) kg = 200 kg.
20. Answer: Option D
Explanation: From I, we conclude that H is the only daughter of M. But this does not indicate that M has no son. The information given in II is immaterial.
21. Answer: Option E
Explanation: Clearly, the company intends to reduce the gap between income and expenditure by increasing the price of its product i.e. by keeping the expenditure unaltered and increasing the income only. So, II is implicit while I is not. However, the rival companies may or may not follow the same pursuit. So, III is not implicit.
22. Answer: Option D
Explanation: The statement expresses grave concern over the lack of proper premises and inadequate staff in labour and industrial courts. This implies that adequate staff is a must to serve the purpose of these courts and a proper office only can ensure their smooth functioning. So, both I and III are implicit. The lack of facilities to the courts also indicates the state's negligent attitude to the condition of the courts. So, II is also implicit.
23. Answer: Option C
Explanation: Clearly, a company would highlight only that feature in its advertisement which people crave for and which it can make possible. So, both I and III are implicit. Nothing can be deduced about the growth of computer industry. So, II is not implicit.
24. Answer: Option A
Explanation: Clearly, since Pramod decides to get the reservation in May for the journey in July, so I is implicit. The number of trains to Madras or the position of vacancies in different classes cannot be deduced from the given statement. So, neither II nor III is implicit.
25. Answer: Option C
Explanation: Since the consultant talks of borrowing money from financial institutions, so I is implicit. That the owners wish to make the company 'commercially viable' makes II implicit. Also, it is mentioned that staff strength is to be reduced to make the company 'commercially viable'. So, III is not implicit.
26. Answer: Option C
Explanation:

27. Answer: Option B
28. Answer: Option A
29. Answer: Option D
30. Answer: Option D
31. Answer: Option A
Explanation:
32. Answer: Option C
33. Answer: Option D
34. Answer: Option E
35. Answer: Option B
36. Answer: Option C
Explanation: B>D>A>E>C>F Here A got 205 marks and he score more marks than E. E score more marks than C & F. C score 160 marks than F. F score minimum marks. The one who got maximum marks, got 100 marks more than C, hence maximum marks will be 160 + 100 = 260
37. Answer: Option B
Explanation: The arrangement is as follows - B>D>A>E>C>F Here A got 205 marks and he score more marks than E. E score more marks than C & F. C score 160 marks than F. F scoe minimum marks.
38. Answer: Option C
Explanation: The arrangement is as follows - B>D>A>E>C>F Here A got 205 marks and he score more marks than E. E score more marks than C & F. C score 160 marks than the possible number of marks which E got will be 185.
39. Answer: Option C
Explanation:
40. Answer: Option B
41. Answer: Option A
42. Answer: Option B
43. Answer: Option B
44. Answer: Option A
Explanation:
45. Answer: Option C
Explanation:
46. Answer: Option D
47. Answer: Option B
48. Answer: Option E
49. Answer: Option C
Explanation:
50. Answer: Option A