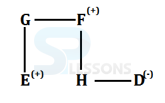Introduction
Introduction
Aspirants of IBPS RRB Officers Scale I 2019, who are willing to enhance their career with banking sector can check all the details in IBPS RRB Officers Scale I – Official Notification issued by IBPS. The online examination Preliminary is scheduled to be conducted in 3[latex]^{rd}[/latex], 4[latex]^{th}[/latex] & 11[latex]^{th}[/latex] August, 2019 (Tentatively), Mains exam is scheduled to be conducted on 22[latex]^{nd}[/latex] September 2019.
Click Here - For Official Website
Candidates planning to take up employment in the Banking sector must be aware of many of the terms policies and other such important information related to Prelims. The article IBPS RRB Officers Scale I Prelims Model Paper provides pattern Questions, and it helps the candidates to devise effective preparation strategies, by focusing on their strengths and weaknesses in different topics and also useful to the candidates while preparing Various Insurance, Banking & Government Exams like SBI PO, SBI Clerk, SSC CPO, SSC CHSL, LIC ADO, LIC AAO.
Preliminary Examination is important to qualify for the Mains Examination. Below mentioned data gives an overview of the IBPS RRB Officers Scale I Prelims Model Paper. The paper is divided into two sections i.e., Reasoning Ability and Quantitative Aptitude.
Note: Every correct answer earns "1" mark and every wrong answer has a penalty of "0.25" i.e.,. 0.25 marks are deducted for every wrong answer.
 Pattern
Pattern
Directions (Q1 - Q3): In each of the questions below are given three statements, followed by conclusions: I, II, III, IV. Read the conclusions and then decide which of the given conclusions logically follows from the given statements.
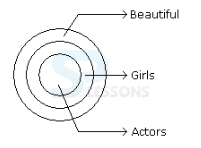
Q1. Statements: All the actors are girls. All the girls are beautiful.
Conclusions:
I. All the actors are beautiful.
II. Some girls are actors.
20. Answer - Option B
Explanation -
Soniya (-) Sona, (+) Sneha (-) Seeta (+) Savita (-) Sarangi (+) Samaira (-) Sajna (+)
21. Answer - Option D
Explanation -
22. Answer - Option B
Explanation -
23. Answer - Option C
Explanation -
24. Answer - Option A
Explanation -
R[65] > K > T[49] > N > P > X[26]
25. Answer - Option
Explanation -
R[65] > K > T[49] > N > P > X[26]
26. Answer - Option B
Explanation -
R[65] > K > T[49] > N > P > X[26]
27. Answer - Option C
Explanation -
R[65] > K > T[49] > N > P > X[26]
28. Answer - Option E
Explanation -
R[65] > K > T[49] > N > P > X[26]
29. Answer - Option C
Explanation -
Check each option, no need to check option D because in D A becomes a male
In C option – B is son of C and C sister of A
30. Answer - Option E
Explanation -
This says that woman’s mother has 2 brothers. And they are women’s maternal uncle.
The boy can be son too and son of woman’s brother too.
31. Answer - Option D
Explanation -
My son’s wife’s daughter will be my granddaughter, and my granddaughter’s mother will be my daughter-in-law. So I m father-in-law of lady.
32. Answer - Option D
Explanation -
Can be sister or cousin sister, because it is not known that how many sons does Sagar’s grandfather have.
33. Answer - Option E
Explanation -
L1 = 210m(Given)
From Statement I, L2 = 300m
L1 + L2 = 210m + 300m = 510m
S1 + S2 = ([latex]\frac{D}{T}[/latex]) = [latex]\frac{510}{10}[/latex] = 51m/s
From Statement II,
S2 = 60kmph = 60 * ([latex]\frac{5}{18}[/latex]) = [latex]\frac{50}{3}[/latex] m/s
S1 – S2 = [latex]\frac{510}{30}[/latex] = [latex]\frac{51}{3}[/latex] => S1 - [latex]\frac{51}{3}[/latex] = [latex]\frac{51}{3}[/latex]
S1 = [latex]\frac{101}{3}[/latex] m/s
34. Answer - Option D
Explanation -
From Statement I, Speed of stream = [latex]\frac{1}{3}[/latex] * Man’s speed = Man’s speed = 3 * Speed of stream
From Statement II, Man’s speed = 2 * Speed of stream
35. Answer - Option B
Explanation -
From Statement I,
Number of male officers = x
Number of female officers = [latex]\frac{x}{2}[/latex] – 250
Ratio can’t be calculated from Statement I.
From Statement II,
Number of male officers = x
Number of female officers = x * [latex]\frac{1}{7}[/latex]
Ratio = [latex]\frac{x}{\frac{x}{7}}[/latex] = 7:1
36. Answer - Option D
Explanation -
Principal is not given, We can not find the rate of CI from both statements.
37. Answer - Option C
Explanation -
I ≥ C ≥ Q ≥ B = N ≥ D
38. Answer - Option D
Explanation -
≥, =, ≥, <
39. Answer - Option C
Explanation -
Z ≥ C > Q ≥ B = N ≥ D
40. Answer - Option D
Explanation -
A < B
- A. Only (I) conclusion follows
B. Only (II) conclusion follows
C. Either (I) or (II) follows
D. Neither (I) nor (II) follows
E. Both (I) and (II) follow
- A. Only (I) conclusion follows
B. Only (II) conclusion follows
C. Either (I) or (II) follows
D. Neither (I) nor (II) follows
E. Both (I) and (II) follow
- A. Only (I) conclusion follows
B. Only (II) conclusion follows
C. Either (I) or (II) follows
D. Neither (I) nor (II) follows
E. Both (I) and (II) follow
- A. 38
B. Professor
C. Study
D. 51
E. None of these
- A. 9[latex]^{th}[/latex] from the left
B. 2[latex]^{nd}[/latex] from the right
C. 8[latex]^{th}[/latex] from the left
D. 5[latex]^{th}[/latex] from the right
E. None of these
- A. 38
B. 57
C. Correct
D. Doctor
E. None of these
- A. VEJHFDV
B. WFGINVF
C. VFCIUNG
D. VCGIVNV
E. None of these
- A. GNPSFQ
B. GNORFR
C. EGOPRF
D. FMORFP
E. None of these
- A. RJRUDODL
B. SJRUOFDFM
C. LRDSGDDS
D. RKSTEOEL
E. None of these
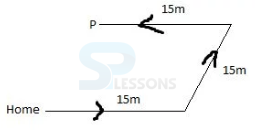
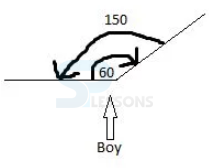
- A. South east and 15
B. north east and 15
C. South west and 15
D. North west and 15
E. None of these
- A. South
B. north
C. east
D. west
E. None of these
- A. North
B. South
C. east
D. west
E. None of these
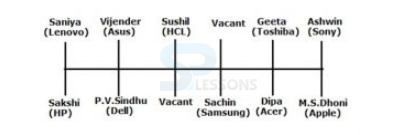
- A. Sakshi
B. Deepa Karmakar
C. M.S.Dhoni
D. Vijender Singh
E. None of these
- A. Saniya Mirza, HCL
B. Dell, Sachin
C. Samsung, M.S.Dhoni
D. Sushilkumar, Toshiba
E. Sakshi, Acer
- A. One
B. Two
C. Three
D. Four
E. More than four
- A. Vijender – HCL
B. P.V.Sindhu – Acer
C. Sakshi – Sony
D. Sachin – Samsung
E. M.S.Dhoni – Toshiba
- A. HCL
B. Acer
C. Sony
D. HP
E. Toshiba
- Sneha likes red and her brother likes pista ice cream. Sajna likes chocolate ice cream and his friend like mango.
- Seeta likes pista ice cream and neither he nor Soniya likes white, yellow, or black. The pink color is liked by a girl and the boy who liked vanilla doesn’t like green color. The one who likes blue eats mint ice cream. Sarangi likes magenta.
- Samaira doesn’t mango or orange ice cream but likes Yellow. Savita doesn’t like white. None of the girls like mango ice cream and none of the boys like strawberry.
- Also, the girl who likes orange ice cream doesn’t like magenta or red. Samaria’s brother Sona doesn’t like Mango ice cream and black color. Soniya doesn’t like blue, and Sneha doesn’t like Butterscotch.
- A. Black
B. Magenta
C. Green
D. White
E. Pista
- A. Sajna
B. Soniya
C. One who likes pink
D. Samaira
E. One who likes red
- A. First from the right end
B. Third from the left end
C. First from the left end
D. Cannot be determined
E. Eight from the left end
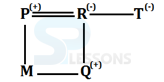
- A. M is nephew of T
B. Q is daughter of P
C. M is son of R
D. T is sister-in-law of P
E. R is brother of P
- A. R$M*O%N@P
B. M$N@O%P*R
C. O%M*R$N@P
D. M$N*O%P@R
E. None of these
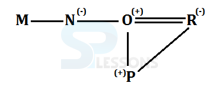
- A. D is niece of G
B. E is cousin of D
C. D is nephew of G
D. F is father of H
E. All are true
- A. X
B. P
C. K
D. T
E. R
- A. 66yr
B. 60yr
C. 49yr
D. 45yr
E. None of these
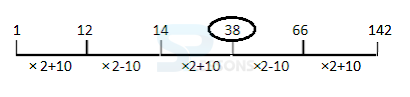
- A. 36
B. 38
C. 31
D. 26
E. Can’t be determined
- A. N
B. T
C. P
D. both (B) or (C)
E. None of these
- A. T
B. R
C. P
D. N
E. Either (C) or (D)
- A. B*C&A
B. A*C&B
C. B&C*A
D. A&C*B
E. C*B&A
- A. Nephew
B. Son
C. Brother-in-law
D. Grandson
E. Son or Nephew
- A. Son
B. Uncle
C. Father
D. Father-in-law
E. None of these
- A. Daughter
B. Sister
C. Cousin Sister
D. Data inadequate
E. None of these
- A. If the data in statement I alone is sufficient to answer the question.
B. If the data in statement II alone are sufficient to answer the question.
C. If the data either in statement I alone or statement II alone are sufficient to answer the question.
D. If the data given in both I and II together are not sufficient to answer the question.
E. If the data in both the statements I and II together are necessary to answer the question.
- A. If the data in statement I alone is sufficient to answer the question.
B. If the data in statement II alone are sufficient to answer the question.
C. If the data either in statement I alone or statement II alone are sufficient to answer the question.
D. If the data given in both I and II together are not sufficient to answer the question.
E. If the data in both the statements I and II together are necessary to answer the question.
- A. If the data in statement I alone is sufficient to answer the question.
B. If the data in statement II alone are sufficient to answer the question.
C. If the data either in statement I alone or statement II alone are sufficient to answer the question.
D. If the data given in both I and II together are not sufficient to answer the question.
E. If the data in both the statements I and II together are necessary to answer the question.
- A. If the data in statement I alone is sufficient to answer the question.
B. If the data in statement II alone are sufficient to answer the question.
C. If the data either in statement I alone or statement II alone are sufficient to answer the question.
D. If the data given in both I and II together are not sufficient to answer the question.
E. If the data in both the statements I and II together are necessary to answer the question.
- A. K ≥ I ≤ R = P < S ≤ D
B. U ≥ D ≥ M = F ≤ A ≥ I
C. I ≥ C ≥ Q ≥ B = N ≥ D
D. G ≥ I = A < B ≤ S ≤ D
E. D ≥ E = G ≥ W = Y ≥ I
- A. >, ≥, <, =
B. >, >, ≥, <
C. ≥, ≥, ≥, ≤
D. ≥, =, ≥, <
E. Other than those given as options
- A. K ≥ Z ≤ R = P < S ≤ D
B. U ≥ D ≥ M = F ≤ A ≥ Z
C. Z ≥ C > Q ≥ B = N ≥ D
D. G ≥ Z = A < B ≤ S ≤ D
E. D ≥ E = G ≥ W = Y ≥ Z
- A. A ≤ P
B. S < P
C. M > P
D. A < B
E. T ≤ M
| Sneha(-) | Red | Strawberry |
| Savita(-) | Blue | Mint |
| Soniya(-) | Pink | Orange |
| Sarangi(+) | Magenta | Mango |
| Seeta(+) | Green | Pista |
| Sona(+) | White | Vanilla |
| Samaira(-) | Yellow | Butterscotch |
| Sajna(+) | Black | Chocolate |
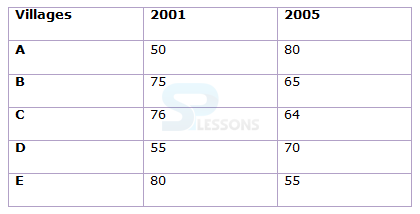
Directions (Q1 - Q2): Study the following information and answer the questions that follow:
The Table given below shows the percentage of valid voters in 5 villages in two years 2001 and 2005. Study the graph carefully to answer the based questions.
NOTE - Total voters in any year = Valid voters + Invalid voters
Q1. What is the difference between invalid voters of village C in the two given years if valid voters in 2005 in that village are 4000 and the ratio of valid voters of village C in 2001 to 2005 is 19: 25?
- A. 1190
B. 1250
C. 1290
D. 1350
E. 1365
- A. 4400
B. 4600
C. 5400
D. 5200
E. 4800
- A. 1440
B. 43200
C. 1440
D. 5420
E. None of these
- A. 4320
B. 1440
C. 720
D. 840
E. None of these
- A. 620
B. 550
C. 520
D. 480
E. 460
- A. 6312
B. 6223
C. 6475
D. 6217
E. 6421
- A. 6 : 5
B. 10 : 9
C. 11 : 9
D. 13 : 12
E. Cannot be determined
- A. 812.5 rupees
B. 912.5 rupees
C. 1012.5 rupees
D. 1112.5 rupees
E. None of these
- A. 18
B. 20
C. 22
D. 24
E. None of these
- A. 7
B. 5
C. 6
D. 4
E. None of these
- A. 137
B. 140
C. 135
D. 120
E. None of these
- A. 10%
B. 20%
C. 17%
D. 15%
E. None of these
- A. 39 days
B. 37 days
C. 37 [latex]\frac{1}{2}[/latex] days
D. 40 days
E. 39 [latex]\frac{1}{2}[/latex] days
- A. 45
B. 60
C. 35
D. 50
E. 65
- A. 800 m
B. 700 m
C. 650 m
D. 750 m
E. None of these
- A. 8 minutes
B. 6 minutes
C. 10 minutes
D. 4 minutes
E. None of these
- A. 8%
B. 7%
C. 9%
D. 11%
E. None of these
- A. Rs.18000
B. Rs.21000
C. Rs.23000
D. Rs.24000
E. None of these
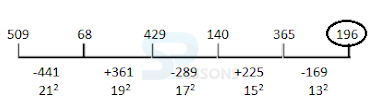
- A. 194
B. 192
C. 196
D. 195
E. 197
- A. 6√2
B. √60
C. 5√3
D. 3√5
E. √50
- A. 48%
B. 50%
C. 40%
D. 53%
E. None of these
- A. Rs.32.64
B. Rs.31.50
C. Rs.30.46
D. Rs.29.75
E. None of these
- A. 23
B. 32
C. 36
D. 34
E. None of these
- A. 31
B. 42
C. 76
D. 81
E. None of these
- A. if P is greater than q.
B. if p is smaller than q.
C. if p is equal to q.
D. if p is either equal to or greater than q.
E. if p is either equal to or smaller than q.
- A. if x < y
B. if x ≤ y
C. relationship between x and y cannot be determined
D. if x ≥ y
E. if x > y
- A. 65
B. 60
C. 67
D. 76
E. None of these
- A. 63
B. 81
C. 72
D. 90
E. None of these
- A. 46
B. 48
C. 44
D. 42
E. None of these
- A. 950
B. 930
C. 960
D. 970
E. None of these
- A. 52, 12
B. 42, 12
C. 32, 12
D. 54, 14
E. None of these
- A. 12 years
B. 14 years
C. 16 years
D. 18 years
E. None of these
- A. 73.50 kg
B. 74.50 kg
C. 75.50 kg
D. 76.50 kg
E. None of these
- A. 20.5 gm
B. 22.5 gm
C. 25.5 gm
D. 28.5 gm
E. None of these
- A. 15 minutes
B. 25 minutes
C. 35 minutes
D. 45 minutes
E. None of these
- A. 3 m
B. 8 m
C. 9 m
D. 6 m
E. None of these
- A. 1000
B. 2000
C. 3000
D. 4000
E. None of these
- A. 4750
B. 5740
C. 5750
D. 6750
E. None of these
- A. 45
B. 41
C. 51
D. 35
E. None of these
- A. 560
B. 420
C. 860
D. 550
E. None of these
Other Articles
 Study Guide
Study Guide
 Exams
Exams
| Competitive Exams - College Entrance Exams | ||
|---|---|---|
| Category | Notification | |
| Diploma | NITC New Delhi | Goa Diploma Admissions 2019 |
PG |
GATE 2020 |
XAT 2020 |
| Click Here For – All India Entrance Exam Notifications | ||
 Daily CA
Daily CA
 Job-Alerts
Job-Alerts
 SP Quiz
SP Quiz
| Competitive Exams - Practice Sets | |
|---|---|
| Category | Quiz |
| English Language | Spotting Errors |
| Insurance Awareness | Insurance Awareness |
| Quantitative Aptitude | Time and Work |
 GK
GK
| General Knowledge for Competitive Examinations | |
|---|---|
| Topic | Name of the Article |
| GK - World | BCCI Awards List |
| USA Presidents | |
| GK - India | NIRF Rankings 2019 |
| Indian Thermal Power Plants | |
| GK - Abbreviations | Insurance Domain Abbreviations |
| Education Abbreviations | |
| GK - Banking & Insurance | Credit card – Debit card – Smart card |
| Future of Insurance Sector | |
| GK - Science & Technology | Famous Websites |
| Unit of Measurement | |
| Science Branches | |