Partnership
1. Sumit and Ravi started a business by investing Rs 85000 and 15000 respectively. In what ratio the profit earned after 2 years be divided between Sumit and Ravi respectively.
A. 17:1
B. 17:2
C. 17:3
D. 17:4
Answer: Option (C)
Explanation:
Note: If you have a clear concept of ratio and proportion chapter then it will really easy for you to solve partnership problems.
P:Q = 85000:15000 = 17:3
Important to note there that if both have invested for a different period of times then we had to multiply with the number of months to get the desired ratio.
2. A, B, and C enter into a partnership investing Rs 35000, Rs 45000 and 55000. Find their respective shares in annual profit of 40,500.
A. 10500, 13500, 19500
B. 10500, 13500, 18500
C. 10500, 13500, 17500
D. 10500, 13500, 16500
Answer: Option (D)
Explanation:
A:B:C = 35000:45000:55000 = 7:9:11
A's share = (7/27) *40500 = Rs 10500
B's share = (9/27) *40500 = Rs 13500
C's share = (11/27)*40500 = Rs 16500
3. A and B started a partnership business investing some amount in the ratio of 3 : 5. C joined them after six months with an amount equal to that of B. In what proportion should the profit at the end of one year be distributed amount A, B, and C
A. 3:7:5
B. 6:10:5
C. 6:10:7
D. 6:7:5
Answer: Option (B)
Explanation:
Let initial investment of A is 3x and B is 5x, then C investment is also 5x, but most important to note in this question is the time duration of the investment Like, A invested for 12 months, B invested for 12 months and C invested for 6 months.
A:B:C =(3x*12):(5x*12):(5x*6)
= 36:60:30
= 6:10:5
4. Anand and Deepak started a business investing Rs.22,500 and Rs.35,000 respectively. Out of a total profit of Rs. 13,800. Deepak's share is
A. Rs 9600
B. Rs 8500
C. Rs 8450
D. Rs 8400
Answer: Option (D)
Explanation:
Ratio of their shares = 22500: 35000
=9: 14
Deepak's share = Rs.(13800×14/23)
= Rs. 8400.
5. A started a business with Rs.21,000 and is joined afterward by B with Rs.36,000. After how many months did B join if the profits at the end of the year are divided equally?
Answer: Option (B)
Explanation:
Suppose B joined after x months
then,
=21000*12=36000*(12-x)
=> 36x = 180
=> x = 5
Simple Interest
1. A sum of money at simple interest amounts to Rs. 2240 in 2 years and to Rs. 2600 in 5 years. What is the principal amount
A. 1000
B. 1500
C. 2000
D. 2500
Answer: Option (C)
Explanation:
SI for 3 year = 2600-2240 = 360
SI for 2 year 360/3 * 2 = 240
principal = 2240 - 240 = 2000
2. At what rate, percent per annum will the simple interest on a sum of money be 2/5 of the amount in 10 years
Answer: Option (D)
Explanation:
Let sum = x
Time = 10 years.
S.I = 2x /5, [as per question]
Rate =( (100 * 2x) / (x*5*10))%
=> Rate = 4%
3. In how many years Rs 150 will produce the same interest at 8% as Rs. 800 produce in 3 years at 9/2%
Answer: Option (B)
Explanation:
Firstly we need to calculate the SI with principal 800, Time 3 years and Rate 9/2%, it will be Rs. 108
Then we can get the Time as
Time = (100*108)/(150*8) = 9.
4. A sum of money amounts to Rs 9800 after 5 years and Rs 12005 after 8 years at the same rate of simple interest. The rate of interest per annum is
A. 9%
B. 10%
C. 11%
D. 12%
Answer: Option (D)
Explanation:
We can get SI of 3 years = 12005 - 9800 = 2205
SI for 5 years = (2205/3)*5 = 3675 [so that we can get principal amount after deducting SI]
Principal = 12005 - 3675 = 6125
So Rate = (100*3675)/(6125*5) = 12%
5. At 5% per annum simple interest, Rahul borrowed Rs. 500. What amount will he pay to clear the debt after 4 years
A. 750
B. 700
C. 650
D. 600
Answer: Option (D)
Explanation:
We need to calculate the total amount to be paid by him after 4 years, So it will be Principal + simple interest.
So, => 500 + [latex]\frac {500 \times 5 \times 4}{100}[/latex] = 600 Rs.
Discount
1. What is the true discount if a banker’s discount on a bill due 4 months hence is 420 at 15%?
A. 400
B. 410
C. 390
D. 380
Answer: Option (A)
Explanation:
Using the formula:
True Discount = (Banker’s Discount * 100 * 100)+ Total Rate
=> True Discount = 420*100/100+15 = 400
Thus the true discount is Rs 100.
2. A man purchased a cow for Rs. 3000 and sold it the same day for Rs. 3600, allowing the buyer a credit of 2 years. If the rate of interest is 10% per annum, then the man has a gain of:
A. 0%
B. 5%
C. 7.5%
D. 10%
Answer: Option (A)
3. A trader owes a merchant Rs. 10,028 due 1 year hence. The trader wants to settle the account after 3 months. If the rate of interest 12% per annum, how much cash should he pay?
A. Rs. 9025.20
B. Rs. 9200
C. Rs. 9600
D. Rs. 9560
Answer: Option (B)
4. A man buys a watch for Rs. 1950 in cash and sells it for Rs. 2200 at a credit of 1 year. If the rate of interest is 10% per annum, the man:
A. gains Rs. 55
B. gains Rs. 50
C. loses Rs. 30
D. gains Rs. 30
Answer: Option (B)
5. Gopal has to pay Rs.440 to Ajay after 1 year. Ajay asks Gopal to pay Rs.220 in cash and defer the payment of Rs.220 for 2 years. If the rate of interest is 10% per annum, in this mode of payment:
A. Gopal gains Rs.3.33
B. Ajay gains Rs.3.33
C. Ajay loses Rs.16.67
D. Gopal loses Rs.16.67
Answer: Option (B)
Average
1. A batsman makes a score of 87 runs in the 17[latex]^{th}[/latex] match and thus increases his average by 3. Find his average after 17[latex]^{th}[/latex] match
Answer: Option (D)
Explanation:
Let the average after the 17[latex]^{th}[/latex] match is x
then the average before the 17[latex]^{th}[/latex] match is x-3
so 16(x-3) + 87 = 17x
=> x = 87 - 48 = 39
2. The average weight of 10 people increased by 1.5 kg when one person of 45 kg is replaced by a new man. Then the weight of the new man is
Answer: Option (C)
Explanation:
Total weight increased is 1.5 * 10 = 15.
So the weight of the new person is 45+15 = 60
3. Average of five numbers is 27. If one number is excluded the average becomes 25. The excluded number is
Answer: Option (A)
Explanation:
Number is (5*27) - (4*25) = 135-100 = 35
4. Average of all prime numbers between 30 to 50
A. 37
B. 37.8
C. 39
D. 39.8
Answer: Option (D)
Explanation:
Prime numbers between 30 and 50 are: 31, 37, 41, 43, 47
Average of prime numbers between 30 to 50 will be
[latex]\frac{31+37+41+43+47}{5}[/latex]
=[latex]\frac{199}{5}[/latex]
=39.8
5. The average age of husband, wife and their child 3 years ago was 27 years and that of wife and the child 5 years ago was 20 years. The present age of the husband is
Answer: Option (A)
Explanation:
Sum of the present ages of husband, wife and child = (27 * 3 + 3 * 3) years = 90 years.
Sum of the present ages of wife and child = (20 * 2 + 5 * 2) years = 50 years.
Husband's present age = (90 - 50) years = 40 years
Time & Work
1. A, B and C can do a piece of work in 7 days, 14 days and 28 days respectively. How long will they taken, if all the three work together?
A. 3 days
B. 4 days
C. 5 days
D. 6 days
Answer: Option (B)
Explanation:
1/7 + 1/14 + 1/28 = 7/28 = 1/4 => 4 days
2. After working for 6 days, Ashok finds that only 1/3 rd of the work has been done. He employs Ravi who is 60% as efficient as Ashok. How many days more would Ravi take to complete the work?
A. 19 days
B. 10 days
C. 20 days
D. 12 days
Answer: Option (C)
Explanation:
1/3 ---- 6
1 -------? A = 18
R = 1/18 * 60/100 = 1/30
1 ----- 1/30
2/3 ----? => 20 days
3. A, B, and C can do a work in 6, 8 and 12 days respectively doing the work together and get a payment of Rs.1800. What is B’s share?
A. Rs.600
B. Rs.450
C. Rs.300
D. Rs.500
Answer: Option (A)
Explanation:
WC = 1/6:1/8:1/12 => 4:3:2
3/9 * 1800 = 600
4. If A, B, and C together can finish a piece of work in 4 days. A alone in 12 days and B in 18 days, then C alone can do it in?
A. 21 days
B. 15 days
C. 12 days
D. 9 days
Answer: Option (D)
Explanation:
C = 1/4 - 1/12 – 1/18 = 1/9 => 9 days
5. 5 men and 12 boys finish a piece of work in 4 days, 7 men and 6 boys do it in 5 days. The ratio between the efficiencies of a man and boy is?
A. 1:2
B. 2:1
C. 2:3
D. 6:5
Answer: Option (D)
Explanation:
5M + 12B ----- 4 days
7M + 6B ------- 5 days
20M + 48B = 35M + 30B
18B = 15M => 5M = 6B
M: B = 6:5
Permutation and Combination
1. In how many different ways can the letters of the word 'OPTICAL' be arranged so that the vowels always come together?
A. 120
B. 720
C. 4320
D. 2160
E. None of these
Answer: Option (B)
Explanation:
The word 'OPTICAL' contains 7 different letters.
When the vowels OIA are always together, they can be supposed to form one letter.
Then, we have to arrange the letters PTCL (OIA).
Now, 5 letters can be arranged in 5! = 120 ways.
The vowels (OIA) can be arranged among themselves in 3! = 6 ways.
Required number of ways = (120 x 6) = 720.
2. In how many different ways can the letters of the word 'MATHEMATICS' be arranged so that the vowels always come together?
A. 10080
B. 4989600
C. 120960
D. None of these
Answer: Option (C)
Explanation:
In the word 'MATHEMATICS', we treat the vowels AEAI as one letter.
Thus, we have MTHMTCS (AEAI).
Now, we have to arrange 8 letters, out of which M occurs twice, T occurs twice and the rest are different.
Number of ways of arranging these letters =[latex]\frac {8!}{(2!)(2!)}[/latex] = 10080.
Now, AEAI has 4 letters in which A occurs 2 times and the rest are different.
The number of ways of arranging these letters = [latex]\frac{4!}{2!}[/latex] = 12.
Required number of words = (10080 x 12) = 120960.
3. In how many different ways can the letters of the word 'LEADING' be arranged in such a way that the vowels always come together?
A. 360
B. 480
C. 720
D. 5040
E. None of these
Answer: Option (C)
Explanation:
The word 'LEADING' has 7 different letters.
When the vowels EAI are always together, they can be supposed to form one letter.
Then, we have to arrange the letters LNDG (EAI).
Now, 5 (4 + 1 = 5) letters can be arranged in 5! = 120 ways.
The vowels (EAI) can be arranged among themselves in 3! = 6 ways.
Required number of ways = (120 x 6) = 720.
4. In how many different ways can the letters of the word 'CORPORATION' be arranged so that the vowels always come together?
A. 810
B. 1440
C. 2880
D. 50400
E. 5760
Answer: Option (D)
Explanation:
In the word 'CORPORATION', we treat the vowels OOAIO as one letter.
Thus, we have CRPRTN (OOAIO).
This has 7 (6 + 1) letters of which R occurs 2 times and the rest are different.
The number of ways arranging these letters =[latex]\frac{7!}{2!}[/latex] = 2520.
Now, 5 vowels in which O occurs 3 times and the rest are different, can be arranged
in [latex]\frac{5!}{3!}[/latex] = 20 ways.
Required number of ways = (2520 x 20) = 50400.
5. In how many ways can the letters of the word 'LEADER' be arranged?
A. 72
B. 144
C. 360
D. 720
E. None of these
Answer: Option (C)
Explanation:
The word 'LEADER' contains 6 letters, namely 1L, 2E, 1A, 1D and 1R.
Required number of ways = [latex]\frac{6!}{(1!)(2!)(1!)(1!)(1!)}[/latex] = 360.
Linear Equation
1. Customers are asked to stand in the lines. If one customer is extra in a line, then there would be two less lines. If one customer is less in line, there would be three more lines. Find the number of students in the class.
Answer: Option (C)
2. 8 girls and 12 boys can finish work in 10 days while 6 girls and 8 boys can finish it in 14 days. Find the time taken by the one girl alone that by one boy alone to finish the work.
A. 120, 130
B. 140,280
C. 240,280
D. 100,120
Answer: Option (B)
3. The sum of two digits and the number formed by interchanging its digit is 110. If ten is subtracted from the first number, the new number is 4 more than 5 times the sum of the digits in the first number. Find the first number.
Answer: Option (C)
4. A fraction becomes. when subtracted from the numerator and it becomes. when 8 is added to its denominator. Find the fraction.
A. 4/12
B. 3/13
C. 5/12
D. 11/7
Answer: Option (C)
5. Five years ago, A was thrice as old as B and ten years later, A shall be twice as old as B. What is the present age of A.
Answer: Option (B)
Ratio & Proportion
1. A ratio equivalent to 3 : 7 is:
A. 3 : 9;
B. 6 : 10;
C. 9 : 21;
D. 18 : 49
Answer: Option (C)
2. The ratio 35 : 84 in simplest form is:
A. 5 : 7;
B. 7 : 12;
C. 5 : 12;
D. none of these
Answer: Option (C)
3. In class, there are 20 boys and 15 girls. The ratio of boys to girls is:
A. 4: 3;
B. 3: 4;
C. 4: 5;
D. none of these
Answer: Option (A)
4. Two numbers are in the ratio 7: 9. If the sum of the numbers is 112, then the larger number is:
A. 49;
B. 72;
C. 63;
D. 42
Answer: Option (C)
5. The ratio of 1.5 m to 10 cm is:
A. 1 : 15;
B. 15 : 10;
C. 10 : 15;
E. 15 : 1
Answer: Option (D)
Number Systems
1. What is the unit digit in 584 x 428 x 667 x 213 ?
Answer: Option (A)
Explanation:
Multiply unit digits of each number. Unit digit in 584 x 428 x 667 x 213 = Unit digit in 4 x 8 x 7 x 3. = Unit digit in 672. = 2.
2. 14927 x 567 - 14927 x 467 = y. What is y?
A. 2985400
B. 1492700
C. 7463500
D. 7483500
Answer: Option (B)
Explanation:
y = 14927 x 567 - 14927 x 467 = 14927 x (567 - 467) = 14927 x 100 = 1492700.
3. Which of the following numbers are divisible by 3 but not by 9?
A. 936
B. 39987
C. 2343
D. 36
Answer: Option (C)
Explanation:
For this, calculate the sum of digits:
936: Sum of digits = 18 i.e. divisible by 3 and 9.
39987: Sum of digits = 36 i.e. divisible by 3 and 9.
2343: Sum of digits = 12 i.e. divisible by 3, but not by 9.
36: Sum of digits = 9 i.e. divisible by 3 and 9.
4. Which of the numbers is exactly divisible by 3?
A. 415591
B. 6472
C. 3364
D. 413976
Answer: Option (D)
Explanation:
Divisibility by 3: if the sum of the digits is divisible by 3 then the original number is divisible by 3. 413976, the sum of digits is 30 thus the number is divisible by 3.
5. 20 + 15 X 3.5 = ?
A. 72
B. 72.5
C. 62.5
D. none of these
Answer: Option (B)
Explanation:
= 20 + 15 x 3.5
= 20 + 15 x (7/2)
= 20 + 52.5
= 72.5.
Decimal and Fractions
1. What will be the vulgar fraction of 0.75
A. 3/5
B. 3/4
C. 3/2
D. 3/7
Answer: Option (B)
Explanation:
0.75 = 75/100 = 3/4
2. What will be a vulgar fraction of 0.0056
A. 7/1150
B. 7/1175
C. 7/1250
D. 7/1275
Answer: Option (C)
3. Arrange the fractions in ascending order
A. 5/8 < 7/12 < 3/4< 13/16
B. 5/8 < 7/12 < 13/16 < 3/4
C. 5/8 < 3/4< 13/16 < 7/12
D. 7/12 < 5/8 < 3/4< 13/16
Answer: Option (D)
Explanation:
5/8 = .625, 7/12 = .5833, 3/4 = .75, 13/16 = .8125
So order will be
7/12 < 5/8 < 3/4< 13/16.
4. Evaluate 6202.5 + 620.25 + 62.025 + 6.2025 + .62025
A. 6791.59775
B. 6891.59775
C. 6891.59675
D. 5891.59775
Answer: Option (B)
Explanation:
Just we need to take care to put decimal under decimal, rest add in a simple way
5. Evaluate 2.5 / 0.0005
A. 5000
B. 500
C. 50000
D. 50
Answer: Option (A)
Explanation:
2.5 * 10000 / 5 = 25000/5 = 5000.
Percentages
1. Subtracting 10% from X is the same as multiplying X by what number?
A. 80%
B. 90%
C. 10%
D. 50%
Answer: Option (B)
Explanation:
X - (10/100) X = X * ?
? = 90%
2. If the numerator of a fraction is increased by 20% and its denominator is diminished by 25% value of the fraction is 2/15. Find the original fraction.
A. 1/12
B. 1/8
C. 1/6
D. 1/4
Answer: Option (A)
Explanation:
X * (120/100)
---------------- = 2/15
Y * (75/100)
X/Y = 1/12
3. A and B’s salaries together amount to Rs. 2,000. A spends 95% of his salary and B spends 85% of his. If now their savings are the same, what is A’s salary?
A. Rs.500
B. Rs.750
C. Rs.1250
D. Rs.1500
Answer: Option (D)
Explanation:
(5/100) A = (15/100) B
A = 3B
A + B = 2000
4B = 2000 => B = 500
A = 1500
4. A salesman’s terms were changed from a flat commission of 5% on all his sales to a fixed salary of Rs.1000 plus 2.5% commission on all sales exceeding Rs. 4,000. If his remuneration as per the new scheme was Rs. 600 more than that by the previous schema, his sales were worth?
A. Rs. 14,000
B. Rs. 12,000
C. Rs. 30,000
D. Rs. 40,000
Answer: Option (B)
Explanation:
[1000 + (X-4000) * (2.5/100)] - X * (5/100) = 600
X = 12000
5. The tax on a commodity is diminished by 20% but its consumption is increased by 10%. Find the decreasing percentage of the revenue derived from it?
A. 20%
B. 18%
C. 15%
D. 12%
Answer: Option (D)
Explanation:
100 * 100 = 10000
80 * 110 = 8800
10000------- 1200
100 ------- ? = 12%
Fundamental Arithmetical Operations
1. The ratio between the speeds of two trains is 7 : 8. If the second train runs 400 kms in 4 hours, then the speed of the first train is:
A. 70 km/hr
B. 75 km/hr
C. 84 km/hr
D. 87.5 km/hr
Answer: Option (D)
Explanation:
Let the speed of two trains be 7x and 8x km/hr.
Then, 8x = 400/4 = 100
x = 100/8 = 12.5
Speed of first train = (7 x 12.5) km/hr = 87.5 km/hr.
2. A man on tour travels first 160 km at 64 km/hr and the next 160 km at 80 km/hr. The average speed for the first 320 km of the tour is:
A. 35.55 km/hr
B. 36 km/hr
C. 71.11 km/hr
D. 71 km/hr
Answer: Option (C)
Explanation:
Total time taken = (160/64 + 160/80 hrs. = 9/2 hrs.
Average speed = (320 x 2/9) km/hr = 71.11 km/hr.
3. In covering a distance of 30 km, Celine takes 2 hours more than Sam. If Celine doubles his speed, then he would take 1 hour less than Sam. Celine's speed is:
A. 5 kmph
B. 6 kmph
C. 6.25 kmph
D. 7.5 kmph
Answer: Option (A)
Explanation:
Let Celine's speed be x km/hr.
Then, 30/x - 30/2x = 3
6x = 30
x = 5 km/hr.
4. A farmer travelled a distance of 61 km in 9 hours. He travelled partly on foot @ 4 km/hr and partly on bicycle @ 9 km/hr. The distance travelled on foot is:
A. 14 km
B. 15 km
C. 16 km
D. 17 km
Answer: Option (C)
Explanation:
Let the distance travelled on foot be x km.
Then, distance travelled on bicycle = (61 -x) km.
So, x/4 + (61 -x)/9 = 9
9x + 4(61 -x) = 9 x 36
5x = 80
x = 16 km.
5. An aeroplane covers a certain distance at a speed of 240 kmph in 5 hours. To cover the same distance in 1 2/3 hours, it must travel at a speed of:
A. 300 kmph
B. 360 kmph
C. 600 kmph
D. 720 kmph
Answer: Option (D)
Explanation:
Distance = (240 x 5) = 1200 km.
Speed = Distance/Time
Speed = 1200/(5/3) km/hr. [We can write 1 2/3 hours as 5/3 hours]
Required speed = 1200 x 3/5 km/hr = 720 km/hr.
Mensuration
1. Find the area of trapezium whose parallel sides are 20 cm and 18 cm long, and the distance between them is 15 cm.
A. 225 cm[latex]^ {2}[/latex]
B. 275 cm[latex]^ {2}[/latex]
C. 285 cm[latex]^ {2}[/latex]
D. 315 cm[latex]^ {2}[/latex]
E. None of these
Answer: Option (C)
Explanation:
Area of a trapezium = 1/2 (sum of parallel sides) * (perpendicular distance between them) = 1/2 (20 + 18) * (15) = 285 cm[latex]^ {2}[/latex]
2. The ratio of the length and the breadth of a rectangle is 4 : 3 and the area of the rectangle is 6912 sq cm. Find the ratio of the breadth and the area of the rectangle?
A. 1: 96
B. 1: 48
C. 1: 84
D. 1: 68
E. None of these
Answer: Option (A)
Explanation:
Let the length and the breadth of the rectangle be 4x cm and 3x respectively.
(4x)(3x) = 6912
12x[latex]^ {2}[/latex] = 6912
x[latex]^ {2}[/latex] = 576 = 4 * 144 = 2[latex]^ {2}[/latex] * 12[latex]^ {2}[/latex] (x > 0)
=> x = 2 * 12 = 24
Ratio of the breadth and the areas = 3x : 12x[latex]^ {2}[/latex] = 1 : 4x = 1: 96.
3. The length of a rectangular floor is more than its breadth by 200%. If Rs. 324 is required to paint the floor at the rate of Rs. 3 per sq m, then what would be the length of the floor?
A. 27 m
B. 24 m
C. 18 m
D. 21 m
E. None of these
Answer: Option (C)
Explanation:
Let the length and the breadth of the floor be l m and b m respectively.
l = b + 200% of b = l + 2b = 3b
Area of the floor = 324/3 = 108 sq m
l b = 108 i.e., l * l/3 = 108
l[latex]^ {2}[/latex] = 324 => l = 18.
4. An order was placed for the supply of a carpet whose breadth was 6 m and length was 1.44 times the breadth. What be the cost of a carpet whose length and breadth are 40% more and 25% more respectively than the first carpet. Given that the ratio of carpet is Rs. 45 per sq m?
A. Rs. 3642.40
B. Rs. 3868.80
C. Rs. 4216.20
D. Rs. 4082.40
E. None of these
Answer: Option (D)
Explanation:
Length of the first carpet = (1.44)(6) = 8.64 cm
Area of the second carpet = 8.64(1 + 40/100) 6 (1 + 25/100)
= 51.84(1.4)(5/4) sq m = (12.96)(7) sq m
Cost of the second carpet = (45)(12.96 * 7) = 315 (13 - 0.04) = 4095 - 12.6 = Rs. 4082.40
5. The area of a square is equal to five times the area of a rectangle of dimensions 125 cm * 64 cm. What is the perimeter of the square?
A. 600 cm
B. 800 cm
C. 400 cm
D. 1000 cm
E. None of these
Answer: Option (B)
Explanation:
Area of the square = s * s = 5(125 * 64)
=> s = 25 * 8 = 200 cm
Perimeter of the square = 4 * 200 = 800 cm.
Time & Distance
1. Two cars cover the same distance at the speed of 60 and 64 kmps respectively. Find the distance traveled by them if the slower car takes 1 hour more than the faster car.
A. 906 km
B. 960 m
C. 960 km
D. 966 km
Answer: Option (C)
Explanation:
60(x + 1) = 64x
X = 15
60 * 16 = 960 km
2. Two trains each 250 m in length are running on the same parallel lines in opposite directions with the speed of 80 kmph and 70 kmph respectively. In what time will they cross each other completely?
A. 10 sec
B. 11 sec
C. 12 sec
D. 14 sec
Answer: Option (C)
Explanation:
D = 250 m + 250 m = 500 m
RS = 80 + 70 = 150 * 5/18 = 125/3
T = 500 * 3/125 = 12 sec
3. A 180 meter long train crosses a man standing on the platform in 6 sec. What is the speed of the train?
A. 90 kmph
B. 108 kmph
C. 120 kmph
D. 88 kmph
Answer: Option (B)
Explanation:
S = 180/6 * 18/5 = 108 kmph
4. Excluding stoppages, the speed of a train is 45 kmph and including stoppages, it is 36 kmph. Of how many minutes does the train stop per hour?
A. 10 min
B. 11 min
C. 12 min
D. 13 min
Answer: Option (C)
Explanation:
T = 9/45 * 60 = 12
5. A train leaves Delhi at 9 a.m. at a speed of 30 kmph. Another train leaves at 2 p.m. at a speed of 40 kmph on the same day and in the same direction. How far from Delhi, will the two trains meet?
A. 300 km
B. 400 km
C. 600 km
D. None
Answer: Option (C)
Explanation:
D = 30 * 5 = 150
RS = 40 – 30 = 10
T = 150/10 = 15
D = 40 * 15 = 600 km
Use of Tables & Graphs
1. For which state the average number of candidates selected over the years is the maximum?
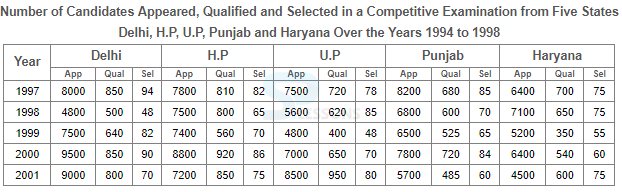
A. Delhi
B. H.P
C. U.P
D. Punjab
Answer: Option (A)
Explanation:
The average number of candidates selected over the given period for various states are:
For Delhi = [latex]\frac {94 + 48 + 82 + 90 + 70}{5}[/latex] = [latex]\frac{384}{5}[/latex] = 76.8.
For H.P. = [latex]\frac{82 + 65 + 70 + 86 + 75}{5}[/latex] = [latex]\frac{378}{5}[/latex] = 75.6.
For U.P. = [latex]\frac{78 + 85 + 48 + 70 + 80}{5}[/latex] = [latex]\frac{361}{5}[/latex] = 72.2.
For Punjab = [latex]\frac{85 + 70 + 65 + 84 + 60}{5}[/latex] = [latex]\frac{364}{5}[/latex] = 72.8.
For Haryana = [latex]\frac{75 + 75 + 55 + 60 + 75}{5}[/latex] = [latex]\frac{340}{5}[/latex] = 68.
Clearly, this average is maximum for Delhi.
2. The percentage of candidates qualified from Punjab over those appeared from Punjab is highest in the year?
A. 1997
B. 1998
C. 1999
D. 2000
Answer: Option (D)
Explanation:
The percentages of candidates qualified from Punjab over those appeared from Punjab during different years are:
For 1997 = ([latex]\frac{680}{8200}[/latex]x 100)% = 8.29%.
For 1998 = ([latex]\frac{600}{6800}[/latex]x 100)% = 8.82%.
For 1999 = ([latex]\frac{525}{6500}[/latex]x 100)% = 8.08%.
For 2000 = ([latex]\frac{720}{7800}[/latex]x 100)% = 9.23%.
For 2001 = ([latex]\frac{485}{5700}[/latex]x 100)% = 8.51%.
Clearly, this percentage is highest for the year 2000.
3. In the year 1997, which state had the lowest percentage of candidates selected over the candidates appeared?
A. Delhi
B. H.P
C. U.P
D. Punjab
Answer: Option (D)
Explanation:
The percentages of candidates selected over the candidates appeared in 1997, for various states are:
(i) For Delhi = ([latex]\frac{94}{8000}[/latex] x 100 ) % = 1.175%.
(ii) For H.P. = ([latex]\frac{82}{7800}[/latex] x 100 ) % = 1.051%.
(iii) For U.P. = ([latex]\frac{78}{7500}[/latex] x 100 ) % = 1.040%.
(iv) For Punjab ([latex]\frac{85}{8200}[/latex] x 100 ) % = 1.037%.
(v) For Haryana ([latex]\frac{75}{6400}[/latex] x 100 ) % = 1.172%.
Clearly, this percentage is the lowest for Punjab.
4. The number of candidates selected from Haryana during the period under review is approximately what percent of the number selected from Delhi during this period?
A. 79.5%
B. 81%
C. 84.5%
D. 88.5%
Answer: Option (D)
Explanation:
Required percentage
=[[latex]\frac{(75 + 75 + 55 + 60 + 75)}{(94 + 48 + 82 + 90 + 70)}[/latex]x 100 ] %
= [[latex]\frac{340}{384}[/latex] x 100 ] %
= 88.54%
≈88.5%
5. What is the approximate percentage of the total number of candidates selected to the total number of candidates qualified for all five states together during the year 1999?
A. 10%
B. 11%
C. 12%
D. 13%
Answer: Option (D)
Explanation:
Required percentage
= [latex]\frac{82 + 70 + 48 + 65 + 55}{640 + 560 + 400 + 525 + 350}[/latex]%
= [[latex]\frac{320}{2475}[/latex] x 100 ]%
= 12.93%
≈ 13%.
Profit & Loss
1. An article is bought for Rs.600 and sold for Rs.500, find the loss percent?
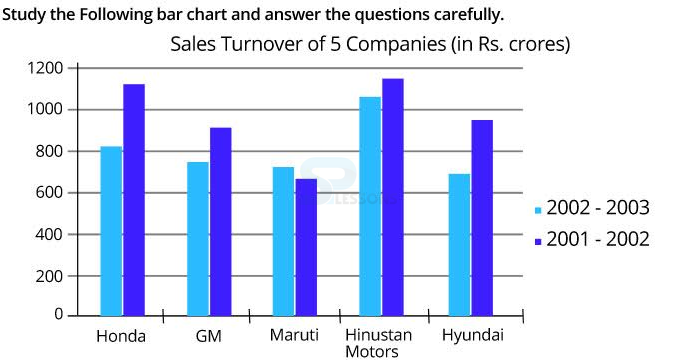
A. 16 4/3%
B. 100/3%
C. 16%
D. 16 2/3%
Answer: Option (D)
Explanation:
600 ---- 100
100 ---- ? => 16 2/3%
2. The cost price of a radio is Rs.1500 and it was sold for Rs.1230, find the loss %?
A. 18%
B. 9%
C. 15%
D. 6%
Answer: Option (A)
Explanation:
1500 ---- 270
100 ---- ? => 18%
3. The sale price sarees listed for Rs.400 after successive discount is 10% and 5% is?
A. Rs.357
B. Rs.340
C. Rs.342
D. Rs.338
Answer: Option (C)
Explanation:
400*(90/100)*(95/100) = 342
4. The list price of an article is Rs.65. A customer pays Rs.56.16 for it. He was given two successive discounts, one of them being 10%. The other discount is?
Answer: Option (B)
Explanation:
65*(90/100)*((100-x)/100) = 56.16
x = 4%
5. Is a single discount equivalent to the discount series of 20%, 10% and 5% is?
A. 25%
B. 30%
C. 31.6%
D. 33.5%
Answer: Option (C)
Explanation:
100*(80/100)*(90/100)*(95/100) = 68.4
100 - 68.4 = 31.6.
Data Interpretation
Directions (1 - 5): The following bar graph shows the percentage profit or loss of a company is given by Income and Expenditures(in million US $) of five companies in the year 2001.
1. Which company earned the maximum percentage profit in the year 2001?
Answer: Option (D)
Explanation:
From M = [(30 - 45)/45 * 100]% = -33.33% i.e. %Loss = 33.33%
From N = [(50 - 40)/40 * 100]% = 25% i.e. %Profit = 25%
From P = [(40 - 45)/45 * 100]% = -11.11% i.e. %Loss = 11.11%
From Q = [(40 - 30)/30 * 100]% = 33.33% i.e. %Profit = 33.33%
From R = [(50 - 45)/45 * 100]% = 11.11% i.e. %Profit = 11.11%
Clearly, the company Q earned maximum profit in 2001.
2. The companies M and N together had a percentage profit/loss of :
A. 12% loss
B. 10% loss
C. 10% profit
D. 12% profit
E. There was no loss or profit
Answer: Option (E)
Explanation:
Total income of companies M and N together = (35 + 50) million US $ = 85 million US $
Total expenditure of companies M and N together = (45 + 40) million US $ = 85 million US $
Percent Profit / Loss companies M and N together
% Profit / Loss = [(85 - 85)/85 * 100) = 0%
3. In 2001 what was the approximate percentage of profit/loss of all the five companies taken together?
A. 5% profit
B. 6.5% profit
C. 4% loss
D. 7% loss
E. 10% profit
Answer: Option (A)
Explanation:
Total income of all five companies = (35 + 50 + 40 + 40 + 50) = 215 million US $
Total expenditure of all five companies = (45 + 40 + 45 + 30 + 45) = 205 million US $
% Profit = [(215 - 205)/205 * 100]% = 4.88% ≈ 5%
4. If the income of company Q in 2001 was 10% more than its income in 2000 and the company had earned a profit of 20% in 2000, then its expenditure in 2000(in million US $) was :
A. 28.28
B. 30.30
C. 32.32
D. 34.34
E. 36.36
Answer: Option (B)
Explanation:
Let the income of company Q in 2000 = x million US $
Then, income of Company Q in 2001
= (110/100 x) million US $
110/100 x = 40 => x = (400/11)
i.e. income of company Q in 2000 = (400/11) million US $.
Let the expenditure of company Q in 2000 be E million US $. Then,
20 = [(400/11) - E]/E * 100 [% Profit = 20%]
=> 20 = [(400/11E) - 1] * 100
=> E = 400/11 * 100/120 = 30.30
Expenditure of company Q in 2000 = 30.30 million US $.
5. For company R, if the expenditure had increased by 20% in the year 2001 from the year 2000 and the company had earned a profit of 10% in 2000, what was the company's income in 2000(in million US $)?
A. 35.75
B. 37.25
C. 38.5
D. 41.25
E. 42.75
Answer: Option (D)
Explanation:
Let the expenditure of company R in 2000 be x million US $.
Then, expenditure of company R in 2001
= (120/100 x) million US $.
120/100 x = 45 => x = 37.5
i.e. expenditure of company R in 2000 = 37.5 million US $.
Let the income of company R in 2000 be I million US $.
Then, 10 = (I - 37.5)/37.5 * 100 [% Profit in 2000 = 10%]
=> I - 37.5 = 3.75 => I = 41.25
i.e. Income of company R in 2000 = 41.25 million US $.
Number Series Simplification
1. Look at this series: 7, 10, 8, 11, 9, 12, ... What number should come next?
Answer: Option (B)
Explanation:
This is a simple alternating addition and subtraction series. In the first pattern, 3 is added; in the second, 2 is subtracted.
2. Look at this series: 36, 34, 30, 28, 24, ... What number should come next?
Answer: Option (B)
Explanation:
This is an alternating number subtraction series. First, 2 is subtracted, then 4, then 2, and so on.
3. Look at this series: 22, 21, 23, 22, 24, 23, ... What number should come next?
Answer: Option (C)
Explanation:
In this simple alternating subtraction and addition series; 1 is subtracted, then 2 is added, and so on.
4. Look at this series: 53, 53, 40, 40, 27, 27, ... What number should come next?
Answer: Option (B)
Explanation:
In this series, each number is repeated, then 13 is subtracted to arrive at the next number.
5. Look at this series: 21, 9, 21, 11, 21, 13, 21, ... What number should come next?
Answer: Option (B)
Explanation:
In this alternating repetition series, the random number 21 is interpolated every other number into an otherwise simple addition series that increases by 2, beginning with the number 9.
Problems on Ages, Profit, Loss, and Discount
1. The sum of ages of 5 children born at the intervals of 3 years each is 50 years. What is the age of the youngest child?
A. 4 years
B. 8 years
C. 10 years
D. None of these
Answer: Option (A)
Explanation:
Let the ages of children be x, (x + 3), (x + 6), (x + 9) and (x + 12) years.
Then, x + (x + 3) + (x + 6) + (x + 9) + (x + 12) = 50
5x = 20
x = 4.
Age of the youngest child = x = 4 years.
2. A father said to his son, "I was as old as you are at the present at the time of your birth". If the father's age is 38 years now, the son's age five years back was:
A. 14 years
B. 19 years
C. 33 years
D. 38 years
Answer: Option (A)
Explanation:
Let the son's present age be x years. Then, (38 - x) = x
2x = 38.
x = 19.
Son's age 5 years back (19 - 5) = 14 years.
3. A is two years older than B who is twice as old as C. If the total of the ages of A, B and C be 27, then how old is B?
A. 7
B. 8
C. 9
D. 10
E. 11
Answer: Option (D)
Explanation:
Let C's age be x years. Then, B's age = 2x years. A's age = (2x + 2) years.
(2x + 2) + 2x + x = 27
5x = 25
x = 5.
Hence, B's age = 2x = 10 years.
4. A man is 24 years older than his son. In two years, his age will be twice the age of his son. The present age of his son is:
A. 14 years
B. 18 years
C. 20 years
D. 22 years
Answer: Option (D)
Explanation:
Let the son's present age be x years. Then, man's present age = (x + 24) years.
(x + 24) + 2 = 2(x + 2)
x + 26 = 2x + 4
x = 22.
5. The sum of the present ages of a father and his son is 60 years. Six years ago, father's age was five times the age of the son. After 6 years, son's age will be:
A. 12 years
B. 14 years
C. 18 years
D. 20 years
Answer: Option (D)
Explanation:
Let the present ages of son and father be x and (60 -x) years respectively.
Then, (60 - x) - 6 = 5(x - 6)
54 - x = 5x - 30
6x = 84
x = 14.
Son's age after 6 years = (x+ 6) = 20 years.
Mixture and Allegations
1. A mixture of 150 liters of wine and water contains 20% water. How much more water should be added so that water becomes 25% of the new mixture?
A. 7 liters
B. 15 liters
C. 10 liters
D. 9 liters
Answer: Option (C)
Explanation:
Number of liters of water in150 liters of the mixture = 20% of 150 = 20/100 * 150 = 30 liters.
P litres of water added to the mixture to make water 25% of the new mixture.
Total amount of water becomes (30 + P) and total volume of mixture is (150 + P).
(30 + P) = 25/100 * (150 + P)
120 + 4P = 150 + P => P = 10 liters.
2. Two varieties of wheat - A and B costing Rs. 9 per kg and Rs. 15 per kg were mixed in the ratio 3 : 7. If 5 kg of the mixture is sold at 25% profit, find the profit made?
A. Rs. 13.50
B. Rs. 14.50
C. Rs. 15.50
D. Rs. 16.50
E. None of these
Answer: Option (D)
Explanation:
Let the quantities of A and B mixed be 3x kg and 7x kg.
Cost of 3x kg of A = 9(3x) = Rs. 27x
Cost of 7x kg of B = 15(7x) = Rs. 105x
Cost of 10x kg of the mixture = 27x + 105x = Rs. 132x
Cost of 5 kg of the mixture = 132x/10x (5) = Rs. 66
Profit made in selling 5 kg of the mixture = 25/100 (cost of 5 kg of the mixture) = 25/100 * 66 = Rs. 16.50
3. In a mixture of milk and water, the proportion of milk by weight was 80%. If, in a 180 gm mixture, 36 gms of pure milk is added, what would be the percentage of milk in the mixture formed?
A. 80%
B. 100%
C. 84%
D. 87.5%
E. None of these
Answer: Option (E)
Explanation:
Percentage of milk in the mixture formed = [80/100 (180) + 36] / (180 + 36) * 100% = (144 + 36)/216 * 100% = 5/6 * 100% = 83.33%.
4. In a can, there is a mixture of milk and water in the ratio 4 : 5. If it is filled with an additional 8 litres of milk the can would be full and ratio of milk and water would become 6 : 5. Find the capacity of the can?
A. 40
B. 44
C. 48
D. 52
E. None of these
Answer: Option (B)
Explanation:
Let the capacity of the can be T litres.
Quantity of milk in the mixture before adding milk = 4/9 (T - 8)
After adding milk, quantity of milk in the mixture = 6/11 T.
6T/11 - 8 = 4/9(T - 8)
10T = 792 - 352 => T = 44.
5. A mixture of 70 litres of milk and water contains 10% water. How many litres of water should be added to the mixture so that the mixture contains 12 1/2% water?
A. 2
B. 8
C. 4
D. 5
E. None of these
Answer: Option (A)
Explanation:
Quantity of milk in the mixture = 90/100 (70) = 63 litres.
After adding water, milk would form 87 1/2% of the mixture.
Hence, if quantity of mixture after adding x liters of water, (87 1/2) / 100 x = 63 => x = 72
Hence 72 - 70 = 2 litres of water must be added.
Pipes and Cisterns
1. Two pipes A and B can fill a cistern in 20 and 30 minutes respectively, and a third pipe C can empty it in 40 minutes. How long will it take to fill the cistern if all the three are opened at the same time?
A. 19 1/7 min
B. 15 1/7 min
C. 17 1/7 min
D. 7 1/7 min
Answer: Option (C)
Explanation:
1/20 + 1/30 - 1/40 = 7/120
120/7 = 17 1/7.
2. Two pipes A and B can separately fill a tank in 2 minutes and 15 minutes respectively. Both the pipes are opened together but 4 minutes after the start the pipe A is turned off. How much time will it take to fill the tank?
A. 9 min
B. 10 min
C. 11 min
D. 12 min
Answer: Option (B)
Explanation:
4/12 + x/15 = 1
x = 10
3. A cistern has a leak which would empty the cistern in 20 minutes. A tap is turned on which admits 4 liters a minute into the cistern, and it is emptied in 24 minutes. How many liters does the cistern hold?
A. 480 liters
B. 600 liters
C. 720 liters
D. 800 liters
Answer: Option (A)
Explanation:
1/x - 1/20 = -1/24
x = 120
120 * 4 = 480.
4. Two taps can separately fill a cistern 10 minutes and 15 minutes respectively and when the waste pipe is open, they can together fill it in 18 minutes. The waste pipe can empty the full cistern in?
A. 7 min
B. 13 min
C. 23 min
D. 9 min
Answer: Option (D)
Explanation:
1/10 + 1/15 - 1/x = 1/18
x = 9
5. Two pipes A and B can fill a tank in 4 and 5 hours respectively. If they are turned up alternately for one hour each, the time taken to fill the tank is?
A. 2 hrs 15 min
B. 4 hrs 24 min
C. 5 hrs
D. 3 hrs
Answer: Option (B)
Explanation:
1/4 + 1/5 = 9/20
20/9 = 2 2/9
9/20 * 2 = 9/10 ---- 4 hours
WR = 1 - 9/10 = 1/10
1 h ---- 1/4
? ----- 1/10
2/5 * 60 = 24 = 4 hrs 24 min
Square Roots
1. Perfect square roots between 250 and 300 are
A. 256, 289
B. 252, 279
C. 262, 289
D. 272, 292
Answer: Option (A)
2. Square of 18 is
A. 324
B. 369
C. 144
D. 342
Answer: Option (A)
3. The least perfect square, which is divisible by each of 21, 36 and 66 is:
A. 213444
B. 214344
C. 214434
D. 231444
Answer: Option (A)
Explanation:
L.C.M. of 21, 36, 66 = 2772.
Now, 2772 = 2 x 2 x 3 x 3 x 7 x 11
To make it a perfect square, it must be multiplied by 7 x 11.
So, required number = 2[latex]^{2}[/latex] x 3[latex]^{2}[/latex] x 7[latex]^{2}[/latex] x 11[latex]^{2}[/latex] = 213444.
4. If 3[latex]\sqrt {5}[/latex] + [latex]\sqrt {125}[/latex] = 17.88, then what will be the value of [latex]\sqrt {80}[/latex] + [latex]\sqrt {65}[/latex] ?
A. 13.41
B. 20.46
C. 21.66
D. 22.35
Answer: Option (D)
Explanation:
3[latex]\sqrt {5}[/latex] + [latex]\sqrt {125}[/latex] = 17.88
3[latex]\sqrt {5}[/latex] + [latex]\sqrt {12 \times 5}[/latex] = 17.88
3[latex]\sqrt {5}[/latex] + 5[latex]\sqrt {5}[/latex] = 17.88
8[latex]\sqrt {5}[/latex] = 17.88
[latex]\sqrt {5}[/latex] = 2.235
[latex]\sqrt {80}[/latex] + 6[latex]\sqrt {5}[/latex] = [latex]\sqrt {16 \times 5}[/latex] + 6[latex]\sqrt {5}[/latex]
= 4[latex]\sqrt {5}[/latex] + 6[latex]\sqrt {5}[/latex]
= 10[latex]\sqrt {5}[/latex] = (10 x 2.235) = 22.35.
5. A group of students decided to collect as many paise from each member of group as is the number of members. If the total collection amounts to Rs. 59.29, the number of the member is the group is:
Answer: Option (C)
Explanation:
Money collected = (59.29 x 100) paise = 5929 paise.
Number of members = [latex]\sqrt {5929}[/latex] = 77.
Probability
1. Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket drawn has a number which is a multiple of 3 or 5?
A. [latex]\frac{1}{2}[/latex]
B. [latex]\frac{2}{5}[/latex]
C. [latex]\frac{8}{15}[/latex]
D. [latex]\frac{9}{20}[/latex]
Answer: Option (D)
Explanation:
Here, S = {1, 2, 3, 4, ...., 19, 20}.
Let E = event of getting a multiple of 3 or 5 = {3, 6 , 9, 12, 15, 18, 5, 10, 20}.
P(E) = [latex]\frac{n(E)}{n(S)}[/latex] = [latex]\frac{9}{20}[/latex].
2. In a box, there are 8 red, 7 blue and 6 green balls. One ball is picked up randomly. What is the probability that it is neither red nor green?
A. [latex]\frac{1}{3}[/latex]
B. [latex]\frac{3}{4}[/latex]
C. [latex]\frac{7}{19}[/latex]
D. [latex]\frac{8}{21}[/latex]
E. [latex]\frac{9}{21}[/latex]
Answer: Option (A)
Explanation:
Total number of balls = (8 + 7 + 6) = 21.
Let E = event that the ball drawn is a neither red nor green
= event that the ball drawn is blue.
n(E) = 7.
P(E) = [latex]\frac{n(E)}{n(S)}[/latex] = [latex]\frac{7}{21}[/latex] = [latex]\frac{1}{3}[/latex].
3. Three unbiased coins are tossed. What is the probability of getting at most two heads?
A. [latex]\frac{3}{4}[/latex]
B. [latex]\frac{1}{4}[/latex]
C. [latex]\frac{3}{8}[/latex]
D. [latex]\frac{7}{8}[/latex]
Answer: Option (D)
Explanation:
Here S = {TTT, TTH, THT, HTT, THH, HTH, HHT, HHH}
Let E = event of getting at most two heads.
Then E = {TTT, TTH, THT, HTT, THH, HTH, HHT}.
P(E) = [latex]\frac{n(E)}{n(S)}[/latex] = [latex]\frac{7}{8}[/latex].
4. Two dice are thrown simultaneously. What is the probability of getting two numbers whose product is even?
A. [latex]\frac{1}{2}[/latex]
B. [latex]\frac{3}{4}[/latex]
C. [latex]\frac{3}{8}[/latex]
D. [latex]\frac{5}{16}[/latex]
Answer: Option (B)
Explanation:
In a simultaneous throw of two dice, we have n(S) = (6 x 6) = 36.
Then, E = {(1, 2), (1, 4), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 2), (3, 4),
(3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 2), (5, 4), (5, 6), (6, 1),
(6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
n(E) = 27.
P(E) =[latex]\frac{n(E)}{n(S)}[/latex] = [latex]\frac{27}{36}[/latex] = [latex]\frac{3}{4}[/latex].
5. In a lottery, there are 10 prizes and 25 blanks. A lottery is drawn at random. What is the probability of getting a prize?
A. [latex]\frac{1}{10}[/latex]
B. [latex]\frac{2}{5}[/latex]
C. [latex]\frac{2}{7}[/latex]
D. [latex]\frac{5}{7}[/latex]
Answer: Option (C)
Explanation:
P (getting a prize) = [latex]\frac{10}{(10 + 25)}[/latex] = [latex]\frac{10}{35}[/latex] = [latex]\frac{2}{7}[/latex].
Introduction 
1. For which state the average number of candidates selected over the years is the maximum?
1. Which company earned the maximum percentage profit in the year 2001?