Introduction
Introduction
 Pattern
Pattern
Scheme of Main Examination for recruitment to the post of Upper Division Clerk (UDC) in ESIC is as follows:
- Main Examination is an objective test.
- The test will have four sections.
- The overall test duration is for 2 hour (No separate sectional duration).
- The test contain 200 questions with Maximum of 200 marks.
- The marks obtained in Phase – II will be considered for final selection.
- The candidates will be shortlisted for Phase-III in the ratio of 1:5 i.e. about 5 times the number of vacancies in each category on the basis of their performance in Phase - II.
| Name of the Test (Objective Tests) | No. of Qs. | Max. Marks | Duration | Version |
|---|---|---|---|---|
| General Intelligence and Reasoning | 50 | 50 | 2 hour | Bilingual |
| General Awareness | 50 | 50 | Bilingual | |
| Quantitative Aptitude | 50 | 50 | Bilingual | |
| English Comprehension | 50 | 50 | English | |
| Total | 100 | 200 |
 Syllabus
Syllabus
[Click Here] for ESIC UDC Quantitative Aptitude Syllabus
 Samples
Samples
Partnership
1. A, B and C started a business by investing Rs. 1,20,000, Rs. 1,35,000 and ,Rs.1,50,000 respectively. Find the share of each, out of an annual profit of Rs. 56,700.
- A. 1500,1300,1200
B. 12345,12354,18967
C. 16800,18900,21000
D. 12300,11500,17300
- A. 6600,6600,3300
B. 6660,6660,3330
C. 6620,6670,3340
D. 3600,3600,6600
- A. 20400,20500,18700
B. 21500,22600,21700
C. 20500,21200,28200
D. 21900,22700,27300
- A. 1200
B. 1400
C. 1600
D. 1800
- A. 3000
B. 3200
C. 3250
D. 3300
- A. Rs. 650
B. Rs. 690
C. Rs. 698
D. Rs. 700
- A. Rs. 4462.50
B. Rs. 8032.50
C. Rs. 8900
D. Rs. 8925
E. None of these
- A. 3.6
B. 6
C. 18
D. Cannot be determined
E. None of these
- A. 3%
B. 4%
C. 5%
D. 6%
E. None of these
- A. Rs. 2000
B. Rs. 10,000
C. Rs. 15,000
D. Rs. 20,000
- A. Rs. 1386
B. Rs. 1764
C. Rs. 1575
D. Rs. 2268
- A. gains Rs. 55
B. gains Rs. 50
C. loses Rs. 30
D. gains Rs. 30
- A. Rs.700
B. Rs.700
C. Rs.495
D. Rs.900
- A. Gopal gains Rs.3.33
B. Ajay gains Rs.3.33
C. Ajay loses Rs.16.67
D. Gopal loses Rs.16.67
- A. Rs. 1325
B. Rs. 1300
C. Rs. 1350
D. Rs. 1500
- A. 280
B. 285
C. 290
D. 295
- A. 36
B. 37
C. 38
D. 39
- A. 50
B. 55
C. 60
D. 65
- A. 35
B. 45
C. 55
D. 65
- A. 33.25
B. 32.25
C. 34.25
D. 34.50
- A. 11 days
B. 12 days
C. 13 days
D. 14 days
- A. 4 days
B. 6 days
C. 8 days
D. 10 days
- A. 20days
B. 40 days
C. 50 days
D. 60 days
- A. 17 men
B. 14 men
C. 13 men
D. 16 men
- A. 25
B. 24
C. 23
D. 21
- A. 72
B. 144
C. 360
D. 720
E. None of these
- A. 5
B. 10
C. 15
D. 20
- A. 266
B. 5040
C. 11760
D. 86400
E. None of these
- A. 63
B. 90
C. 126
D. 45
E. 135
- A. 40
B. 400
C. 5040
D. 2520
- A. 2x - 7 = 17
B. 2(x - 7) = 17
C. 7 - 2x = 17
D. 7(2 - x) = 17
- A. x - 21 = -19
B. -19 + x = -21
C. x = -19 + 21
D. -19 - 21 = x
- A. 10 + x = 15
B. 10 - x = 15
C. x - 10 = 15
D. 15 - 10 = x
- A. [latex]\frac{x}{24}[/latex] = 4
B. 24 - x = 4
C. 24x = 4
D. [latex]\frac{24}{x}[/latex] = 4
- A. 7
B. 23
C. 19
D. 11
- A. 18
B. 12
C. 9
D. 4
- A. 2
B. 3
C. 4
D. 6
- A. Rs 10
B. Rs 20
C. Rs 24
D. Rs 28
- A. 420
B. 520
C. 620
D. 720
- A. 20 litres
B. 30 litres
C. 50 litres
D. 60 litres
- A. 3200
B. 3600
C. 4000
D. 4200
- A. 4, 0
B. 0, 4
C. 4, 4
D. 1, 1
- A. 3001
B. 2893
C. 2704
D. 2890
- A. 8
B. 9
C. 10
D. 11
- A. 5
B. 9
C. 4
D. 0
- A. 288.946
B. 298.946
C. 198.946
D. 188.946
- A. 47.95
B. 44.95
C. 43.95
D. 40.95
- A. 0.144
B. 0.0144
C. .00144
D. 1.44
- A. 80
B. 800
C. 8000
D. 80000
- A. 6/7, 8/9, 7/8, 9/10
B. 9/10, 7/8, 8/9, 6/7
C. 6/7, 7/8, 8/9, 9/10
D. 9/10, 8/9, 7/8, 6/7
- A. 1/4
B. 1/5
C. 1/10
D. None of above
- A. 1/20
B. 1/50
C. 1/75
D. 1/25
- A. 50 %
B. 125 %
C. 25 %
D. None of the above
- A. 2.09%
B. 20.9%
C. 209%
D. 0.209%
- A. 5
B. 0.5
C. 0.05
D. 0.005
- A. 1 hour
B. 2 hours
C. 3 hours
D. 4 hours
- A. 220 km
B. 224 km
C. 230 km
D. 234 km
- A. 17 6/7 km/hr
B. 25 km/hr
C. 30 km/hr
D. 35 km/hr
- A. 5 kmph
B. 6 kmph
C. 6.25 kmph
D. 7.5 kmph
- A. 14 km
B. 15 km
C. 16 km
D. 17 km
- A. 77.14 cm
B. 47.14 cm
C. 84.92 cm
D. 94.94 cm
E. 23.57 cm
- A. 10
B. 100
C. 1000
D. 10000
E. None of these
- A. Rs. 4800
B. Rs. 3600
C. Rs. 3560
D. Rs. 4530
E. None of these
- A. 252 m
B. 704 m
C. 352 m
D. 808 m
E. None of these
- A. 140
B. 156
C. 175
D. 214
E. None of these
- A. 100 m
B. 150 m
C. 190 m
D. 200 m
- A. 50 sec
B. 52 sec
C. 54 sec
D. 56 sec
- A. 35.55 km/hr
B. 36 km/hr
C. 71.11 km/hr
D. 71 km/hr
- A. 4 hours
B. 4 hours 30 minutes
C. 4 hours 45 minutes
D. 5 hours
- A. 600
B. 750
C. 1000
D. 1250
- A. 128
B. 112
C. 96
D. 88
- A. 1312
B. 1192
C. 1088
D. 968
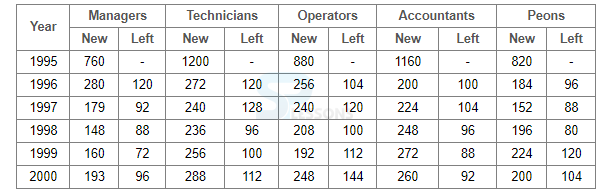
- A. Managers
B. Technicians
C. Operators
D. Accountants
- A. 1325
B. 1195
C. 1265
D. 1235
- A. 19%
B. 21%
C. 27%
D. 29%
- A. No profit, no loss
B. 5%
C. 8%
D. 10%
- A. 100%
B. 200%
C. 300%
D. 400%
- A. 600
B. 1200
C. 1800
D. none of these
- A. 150%
B. 200%
C. 300%
D. 350%
- A. 30 dozens
B. 40 dozens
C. 50 dozens
D. 60 dozens
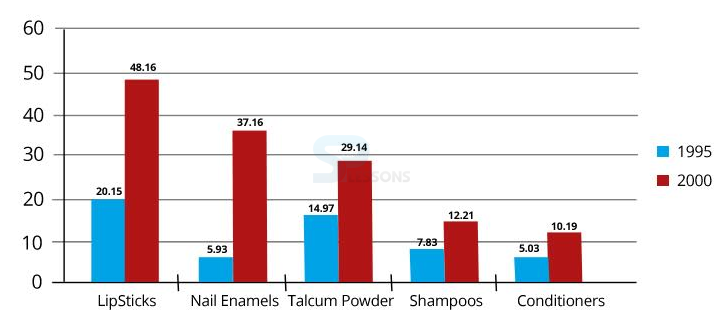
- A. Lipsticks
B. Nail Enamels
C. Talcum Powders
D. Shampoos
E. Conditioners
- A. Lipsticks
B. Nail Enamels
C. Talcum powders
D. Shampoos
E. Conditioners
- A. 33%
B. 31%
C. 28%
D. 22%
E. 21%
- A. 57%
B. 36%
C. 29%
D. 25%
E. 21%
- A. 7:2
B. 5:2
C. 4:3
D. 2:1
E. 5:3
- A. 25 22
B. 26 23
C. 26 24
D. 25 23
E. 26 22
- A. 13 11
B. 10 5
C. 13 8
D. 12 7
E. 10 8
- A. 22 35
B. 35 19
C. 19 35
D. 19 24
E. 22 24
- A. 21 23
B. 20 21
C. 20 17
D. 25 27
E. 22 20
- A. 60 72
B. 50 62
C. 50 72
D. 62 62
E. 62 80
- A. 24.5
B. 25.5
C. 26.5
D. 27.5
- A. 4:3
B. 12:11
C. 7:4
D. 6:5
- A. 11/P + 6
B. P/11 +6
C. 17 - P/6
D. 17/P
- A. 50 yrs
B. 60 yrs
C. 70 yrs
D. 65 yrs
- A. 19 years
B. 17 years
C. 15 years
D. data inadequate
- A. 16: 5
B. 14: 5
C. 16: 7
D. 19: 5
E. None of these
- A. 72
B. 72.9
C. 73.8
D. 74.7
E. None of these
- A. 3:2
B. 3:4
C. 3:5
D. 4:5
- A. 1:1
B. 1:3
C. 1:2
D. 7:5
- A. 25 litres
B. 28 litres
C. 30 litres
D. 35 litres
- A. 20 hrs
B. 28 hrs
C. 36 hrs
D. 40 hrs
- A. 81 min
B. 108 min
C. 144 min
D. 192 min
- A. 8
B. 15
C. 16
D. 18
- A. 8.21 min
B. 8 min
C. 8.57 min
D. 8.49 min
- A. 21 min
B. 24 min
C. 20 min
D. 22 min
- A. 5.65
B. 2.7
C. 3.5
D. 6.66
- A. 41
B. 42
C. 43
D. 44
- A. 9
B. 36
C. 81
D. 144
- A. 3[latex]\sqrt{3}[/latex]
B. 8[latex]\sqrt{3}[/latex]
C. 14
D. 14+8[latex]\sqrt{3}[/latex]
- A. 13
B. 12
C. 17
D. 16
- A. 1/2
B. 3/5
C. 9/20
D. 8/15
- A. 5/12
B. 1/6
C. 1/2
D. 7/9
- A. 2/7
B. 5/7
C. 1/5
D. 1/2
- A. 3/4
B. 7/8
C. 1/2
D. 1/4
- A. 1/6
B. 1/2
C. 1/3
D. 1/4