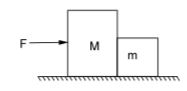
1. Two blocks with masses M and m are in contact with each other and are resting on a horizontal friction-less floor. When horizontal force is applied to the heavier, the blocks accelerate to the right. The force between the two blocks is

A. (M + m) F/m B. MF/m C. mF/M D. mF/(M + m)

Answer - Option D
Explanation -
From free body diagram
F – N = Ma ...(i)
or N = ma ...(ii)
From equations (i) and (ii), we get
N = [latex]\frac{mF}{(m + M)}[/latex]
2. The combined motion of rotation and translation may be assumed to be a motion of pure rotation about some centre which goes on changing from time to time. The centre in question is known as

A. Shear centre B. Meta centre C. Instantaneous centre D. Gravitational centre

Answer - Option C
Explanation -
The instantaneous centre of a link is the point about which all the points on the link appear to rotate at that instant.
3. Two bodies of mass [latex]{m}_{1}[/latex] and [latex]{m}_{2}[/latex] are dropped from different heights [latex]{h}_{1}[/latex] and [latex]{h}_{2}[/latex] respectively. Neglecting the effect of friction, the ratio of times taken to drop through the given heights would be

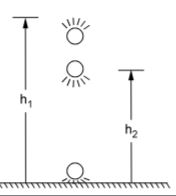
A. [latex]\frac{{m}_{1}}{{m}_{2}}[/latex] B. [latex]\frac{{m}_{1}{h}_{1}}{{m}_{2}{h}_{2}}[/latex] C. [latex]{(\frac{{h}_{1}}{{h}_{2}})}^{\frac{1}{2}}[/latex] D. [latex]{(\frac{{h}_{1}}{{h}_{2}})}^{2}[/latex]

Answer - Option C
Explanation -
s = ut + [latex]\frac{1}{2}g {t}^{2}[/latex]
and u = 0
i.e, [latex]{h}_{1} = \frac{1}{2}g {{t}_{1}}^{2}[/latex], and [latex]{h}_{2} = \frac{1}{2}g {{t}_{2}}^{2}[/latex]
Hence [latex]\frac{{t}_{1}}{{t}_{2}} = {(\frac{{h}_{1}}{{h}_{2}})}^{\frac{1}{2}}[/latex]
4. A block slides down a smooth inclined plane in time t after having been released from its top. An identical block on being released from the same point and falling freely will reach the ground in time

A. [latex]\frac{t}{3}[/latex] B. [latex]\frac{t}{\sqrt{3}}[/latex] C. [latex]\frac{t}{2}[/latex] D. [latex]\frac{t}{4}[/latex]

(Take inclination of plane = 30º)
Answer - Option C
Explanation -
For motion along the plane
a = g sin θ and l = [latex]\frac{h}{sinθ}[/latex]
i.e, [latex]\frac{h}{sin θ} = \frac{1}{2} (g sin θ){t}^{2}[/latex]
or [latex]{t}^{2} = \frac{2h}{g} \frac{1}{{sin}^{2}}θ[/latex] ......(i)
For vertical motion :
h = [latex] \frac{1}{2} g{T}^{2}[/latex]
[latex]{T}^{2} = \frac{2h}{g}[/latex] ......(ii)
From equations (i) and (ii), we get
T = t sin θ = t sin 30º = [latex] \frac{t}{2}[/latex]
5. AB is the vertical diameter of a circle in a vertical plane. Another diameter CD makes an angle of 60º with AB. Then the ratio of time taken by a particle to slide along AB to the time taken by it to slide along CD is

A. 1 : [latex]\sqrt{3} [/latex] B. [latex]\sqrt{2}[/latex] : 1 C. 1 : [latex]\sqrt{2} [/latex] D. [latex]\sqrt{3}[/latex] : [latex]\sqrt{2}[/latex]

Answer - Option C
Explanation -

For motion along the vertical diameter AB
s = d (diameter of circle) and a = g
i.e, d = [latex] \frac{1}{2} g{T}^{2}[/latex]
[latex]{t}^{2} = \frac{2d}{g}[/latex] ......(i)
For motion along the inclined diameter CD,
s = d
and a = g cos 60º = [latex]\frac{g}{2}[/latex]
i.e, d = [latex]\frac{1}{2} *\frac{g}{2} * {T}^{2}[/latex]
or [latex]{T}^{2} = \frac{4d}{g}[/latex] ......(ii)
From equations (i) and (ii) we get
[latex]\frac{t}{T} = \frac{1}{\sqrt{2}}[/latex]
6. Which of the following graphs represents the motion of an objects moving with a linearly increasing acceleration against time ?

A.

B.

C.

D.

Answer - Option B
Explanation -
The acceleration which varies linearly with time
can be expressed as
a = [latex]\frac{dv}{dt}[/latex]= [latex]{a}_{0}[/latex]+ kt
Hence no curve shows with acceleration versus time,
v = [latex]{v}_{0}{a}_{0}t + \frac{k{t}^{2}}{2} [/latex]
Curves (a), (d) are drawn with velocity against time. None of them satisfies the above relations.
However, s = [latex]{s}_{0} + {v}_{0}{a}_{0}t + \frac{{a}_{0}{t}^{2}}{2} + \frac{k{t}^{3}}{6}[/latex]
(B) satisfies this relation
7. Two particles with masses in the ratio 1 : 4 are moving with equal kinetic energies. The magnitude of their linear momentums wil l conform to the ratio

A. 1 : 8 B. 1 : 2 C. [latex]\sqrt{2}[/latex] : 1 D. [latex]\sqrt{2}[/latex]

Answer - Option B
Explanation -
[latex]{(KE)}_{1} = \frac{1}{2} {m}_{1} {{v}_{1}}^{2}[/latex]
[latex]{(KE)}_{1} = \frac{1}{2} {m}_{1} {{v}_{2}}^{2}[/latex]
But kinetic energies are equal and [latex] \frac{{m}_{1}}{{m}_{2}} = \frac{1}{4}[/latex]
Now, [latex]{m}_{1} {{v}_{1}}^{2} = {m}_{2} {{v}_{1}}^{2} [/latex]
[latex] \frac{{v}_{1}}{{v}_{2}} = {(\frac{{m}_{1}}{{m}_{2}})}^{\frac{1}{2}} = 2[/latex]
Required ratio = [latex] \frac{{v}_{1}}{{v}_{2}}\frac{{m}_{1}}{{m}_{2}} = \frac{{v}_{1}}{{v}_{2}} * \frac{{m}_{1}}{{m}_{2}}[/latex]
[latex]\frac{1}{4} * 2 = 1 : 2[/latex]
8. If two bodies one light and other heavy have equal kinetic energies, which one has a greater momentum?

A. Heavy body B. Light body C. Both have equal momentum D. It depends on the actual velocities.

Answer - Option B
Explanation -
Let light body be L and heavy body H
[latex]i.e, \frac{1}{2} {m}_{L} {{v}_{L}}^{2} = \frac{1}{2} {m}_{H} {{v}_{H}}^{2}[/latex]
or [latex] \frac{{m}_{L}}{{m}_{H}} = {\frac{{v}_{H}}{{v}_{L}}}^{2} < 1[/latex]
[latex] \frac{Momentum of light body}{Momentum of heavy body} = \frac{{m}_{L}}{{m}_{H}} \frac{{v}_{H}}{{v}_{L}} = \frac{{v}_{H}}{{v}_{L}}[/latex]
[latex] {\frac{{v}_{H}}{{v}_{L}}}^{2} = \frac{{v}_{H}}{{v}_{L}} < 1[/latex]
Hence momentum of light body is less than the momentum of heavy body or heavier body has greater momentum as compared to lighter body
9. The angular momentum of a system is conserved if there

A. are no forces present B. are no magnetic forces present C. is no net force on the system D. are no torques present

Answer - Option D
Explanation -
Net torque on a system , [latex]\overrightarrow{{r}_{n}}[/latex] = time rate of change of the system’s angular momentum,
i.e.[latex]\overrightarrow{\frac{dl}{dt}}[/latex]
At constant [latex]\overrightarrow{L}[/latex], therefore, [latex]\overrightarrow{{r}_{n}}[/latex] = 0.
10. A body moves along a straight line and the variation of its kinetic energy with time is linear as depicted in the figure below

The force acting on the body is

A. directly proportional to velocity B. inversely proportional to velocity C. zero D. constant

Answer - Option B
Explanation -

Kinetic energy = [latex]\frac{1}{2} m {(\frac{dx}{dt})}^{2} = kt[/latex]
where k is constant
Differentiating, we get
[latex]m \frac{dx}{dt} ({\frac{dx}{dt}}^{2}) = k[/latex]
Force = mass * acceleration
[latex]m {(\frac{dx}{dt})}^{2} = kt (\frac{dx}{dt}) = \frac{k}{v}[/latex]
11. For perfectly elastic bodies, the value of coefficient of restitution is

A. 1 B. 0.5 to 1 C. 0 to 0.5 D. zero

Answer - Option A
Explanation -
Value of coefficient of restitution is unity, if the collision is elastic, i.e. if no energy is dissipated during collision.
Minimum value of coefficient of restitution would be zero for plastic collision, i.e., if energy gets entirely dissipated.
12. A steel ball is dropped from a height [latex]{h}_{1}[/latex] onto a steel plate and rebounds to a height [latex]{h}_{2}[/latex]. The coefficient of restitution between the ball and plate will be

A. [latex]\frac{{h}_{1}}{{h}_{2}}[/latex] B. [latex]\frac{{h}_{1}}{2{h}_{2}}[/latex] C. [latex]\sqrt {\frac{{h}_{1}}{2{h}_{2}}}[/latex] D. [latex]\sqrt {\frac{{h}_{2}}{{h}_{1}}}[/latex]

Answer - Option D
Explanation -
Velocity of ball just before impact, [latex]{v}_{1} = \sqrt {2g{h}_{1}}[/latex]
Its velocity as it rebound, [latex]{v}_{2} = \sqrt {2g{h}_{2}}[/latex]
By definition,
e = [latex]\frac{{v}_{2} - 0}{0 - {v}_{1}} = \frac {\sqrt {2g{h}_{2}}}{-(-\sqrt {2g{h}_{1}})} = \sqrt {\frac{{h}_{2}}{{h}_{1}}}[/latex]
13. Consider a one-dimensional elastic collision between an incoming body A of mass [latex]{m}_{1}[/latex] and a body B of mass [latex]{m}_{2}[/latex] initially at rest. For body B to move with greatest kinetic energy after collision

A. [latex]{m}_{1} > {m}_{2}[/latex] B. [latex]{m}_{1} < {m}_{2}[/latex] C. [latex]{m}_{1} = {m}_{2}[/latex] D. None of these

Answer - Option A
Explanation -
After elastic collision, the velocity of stationary body,
[latex]{{m}_{2}}^{1} = \frac{2{m}_{1}}{{m}_{1} + {m}_{2}}{v}_{1}[/latex]
Kinetic energy = [latex] \frac{1}{2} {m}_{2}{(\frac{2{m}_{1}}{{m}_{1} + {m}_{2}}{v}_{1})}^{2}[/latex]
= [latex]{{v}_{1}}^{2} \frac{2{{m}_{1}}^{2}{m}_{2}}{{({m}_{1} + {m}_{2})}^{2}}[/latex]
Hence kinetic energy will have the greatest possible value when [latex]{m}_{1} > {m}_{2}[/latex]
14. Distance of the centroid of a semicircle of radius r from its base is

A. [latex]\frac{4r}{3\pi}[/latex] B. [latex]\frac{3 \pi}{4r}[/latex] C. [latex]\frac{4 \pi}{3r}[/latex] D. [latex]\frac{2\pi}{3r}[/latex]

Answer - Option A
Explanation -
Area = [latex]\frac{1}{2}\pi {r}_{2}[/latex]
[latex]{x}_{c} = r, {y}_{c} = \frac{4r}{3\pi}[/latex]
15. For maximum horizontal range, the angle of projection of a projectile should be

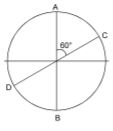
A. 30º B. 45º C. 60º D. 90º

Answer - Option B
Explanation -
Horizontal range, R = [latex]\frac{{{v}_{0}}^{2}sin 2 \alpha}{g}[/latex]
For maximum horizontal range,
sin 2[latex]\alpha[/latex] = 1
or 2[latex]\alpha[/latex] = 90º
or [latex]\alpha[/latex] = 45º

1. Two stones are projected with the same velocity (in magnitudes) but making different angles with the horizontal. If their ranges are equal and the angle of projection of one is 600, then the ratio of the maximum heights attained ( [latex]\frac{{y}_{2}}{{y}_{1}}[/latex]) will be

A. 3 : 1 B. 2 : 1 C. 1 : 2 D. 1 : 3

Answer - Option D
Explanation -
Since ranges and velocities of projection are same and angle of projection of one is 600, therefore angle of projection of the other would be (90º – 60º) = 30º
[latex]\frac{{H}_{2}}{{H}_{1}} = \frac{{{v}_{0}}^{2}{sin}^{2} {\alpha}_{2}}{2g} * \frac {2g}{{{v}_{0}}^{2}{sin}^{2} {\alpha}_{2}}[/latex]
[latex]\frac {{sin}^{2} {\alpha}_{2}}{{sin}^{2}{\alpha}_{1}} = \frac {{sin}^{2} {30º}}{{sin}^{2} {60º} }= 1 : 3[/latex]
2. A stone is projected horizontally from a cliff at 10 m/sec and lands on the ground below at 20 m from the base of the cliff. Find the height h of the cliff. Use g = 10 m/[latex]{sec}^{2}[/latex]

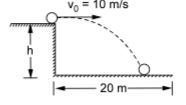
A. 18 m B. 20 m C. 22 m D. 24 m

Answer - Option B
Explanation -

Time of flight = [latex]\frac{20}{10}[/latex] = 2 sec.
Since horizontal component of velocity remains constant, therefore
h = [latex]\frac{1}{2}g {t}^{2}[/latex]
= [latex]\frac{1}{2} * 10 * {2}^{2}[/latex]
= 20 m
3. Two balls are projected from the same point making angles of 600 and 300 with the vertical axis. If both the balls are to attain the same height, the ratio of the speeds of projection ([latex]\frac{{v}_{1}}{{v}_{2}}[/latex]) should be

A. 1 : 2 B. 1 : 1 C. 1 : [latex]\sqrt{3} [/latex] D. [latex]\sqrt{2} : 1[/latex]

Answer - Option C
Explanation -
[latex]\frac{{H}_{2}}{{H}_{1}} = \frac{{{v}_{2}}^{2}{sin}^{2} {\alpha}_{2}}{2g} * \frac {2g}{{{v}_{1}}^{2}{sin}^{2} {\alpha}_{2}}[/latex]
[latex]= {(\frac{{v}_{2}}{{v}_{1}})}^{2} = \frac {{sin}^{2} {30º}}{{sin}^{2} {60º} } = {(\frac{{v}_{2}}{{v}_{1}})}^{2} * \frac {1}{3}[/latex]
But [latex]= {H}_{1} = {H}_{2} [/latex]
i.e, [latex]= \frac{{v}_{1}}{{v}_{2}} = 1 : \sqrt{3} [/latex]
4. For a projectile of range R, the kinetic energy is minimum after the projectile covers (from start) a distance equal to

A. 0.25R B. 0.5R C. 0.75R D. R

Answer - Option B
Explanation -
Kinetic energy is minimum at the point of maximum height, and that height is attained during half of the total time of flight Distance covered
= (horizontal component of velocity) * (half the time of flight)
[latex]{v}_{0} cos \alpha * \frac{2{v}_{0}sin \alpha}{2g} = \frac{{{v}_{0}}^{2} sin2\alpha}{2g}[/latex]
which is half of the range.
5. If the time of flight of a bullet over a horizontal range R is T seconds, the inclination of the direction of projection with the horizontal is

A. [latex]{tan}^{-1}(\frac{g{T}^{2}}{2R})[/latex] B. [latex]{tan}^{-1}(\frac{gT}{2R})[/latex] C. [latex]{tan}^{-1}(\frac{g{T}^{2}}{4R})[/latex] D. [latex]{tan}^{-1}(\frac{2gT}{R})[/latex]

Answer - Option A
Explanation -
R = [latex]\frac{{v}_{0} sin 2\alpha}{g} = {{v}_{0}}^{2} * \frac{2sin\alpha cos\alpha}{g}[/latex]
T = [latex]\frac{2{v}_{0}sin\alpha}{g}[/latex]
[latex]{{V}_{0}}^{2} = \frac{{T}^{2}{g}^{2}}{4 {sin}^{2}\alpha}[/latex]
R = [latex]\frac{{T}^{2}{g}^{2}}{4 {sin}^{2}\alpha} * \frac {2 sin\alpha cos\alpha}{g} = \frac{{T}^{2}{g}}{4 tan\alpha}[/latex]
[latex]\alpha = {tan}^{-1}(\frac{g{T}^{2}}{2R})[/latex]
6. The shaft of a motor starts from rest and attains full speed of 1800 rpm in 10 seconds. The shaft has an angular acceleration of

A. [latex]3 \pi\frac{rad}{{sec}^{2}}[/latex] B. [latex]6 \pi\frac{rad}{{sec}^{2}}[/latex] C. [latex]2 \pi\frac{rad}{{sec}^{2}}[/latex] D. [latex]18 \pi\frac{rad}{{sec}^{2}}[/latex]

Answer - Option B
Explanation -
[latex]\omega = {\omega}_{0} + \alpha t[/latex]
or [latex]\frac{2 \pi * 1800}{60} = 0 + \alpha * t[/latex]
or [latex]\alpha = 6\pi * \frac{rad}{{sec}^{2}}[/latex]
7. A flywheel 200 cm in diameter is rotating at 100 revolutions per minute. A point on the rim of the flywheel will not have

A. angular velocity B. centripetal acceleration C. tangential acceleration D. all of these

Answer - Option C
Explanation -
Since there is no change in magnitude of angular speed, there will be no tangential acceleration.
8. Two bodies of mass M and m are moving in concentric orbits of radii R and r such that their periods are same. Then ratio between their angular velocity is

A. R : r B. mR : Mr C. 1 : 1 D. [latex]\frac{\sqrt{R}}{r} : \frac{m}{M}[/latex]

Answer - Option C
Explanation -
[latex]{T}_{1} = \frac{2\pi}{{\omega}{1}}, {T}_{2} = \frac{2\pi}{{\omega}{2}}[/latex]
i.e, [latex]\frac{{\omega}{2}}{{\omega}{1}} = \frac{{T}_{1}}{{T}_{2}}[/latex]
Since time periods of two bodies are stated to be same, their angular velocities will conform to the ratio 1 : 1
9. A cylinder of radius 10 cm. rolls without slipping on a horizontal plane. At the instant as shown the magnitude of the velocity of A relative to B is 40 cm/sec. The velocity of the centre O at this instant is

A. [latex]10 \sqrt{2}\frac{cm}{sec}[/latex] B. [latex]15 \sqrt{2}\frac{cm}{sec}[/latex] C. [latex]20 \sqrt{2}\frac{cm}{sec}[/latex] D. [latex]25 \sqrt{2}\frac{cm}{sec}[/latex]

Answer - Option C
Explanation -
Velocity = radius * angular velocity
[latex]{V}_{\frac{A}{B}} = {r}_{\frac{A}{B}}\omega = 10 \sqrt{2} \omega = 40\frac{cm}{sec}[/latex]
i.e, [latex]\omega = 2\sqrt{2}\frac{rad}{sec} [/latex]
Thus C is the instant centre of velocity.
i.e, [latex]{V}_{O} = 10\omega = 20 \sqrt{2}{cm}{sec}[/latex]
10. A person standing on a uniformly rotating turn table has his arms held close to his chest. If he outstretches his arms

A. the moment of inertia will decrease B. the angular momentum will increase C. the speed of rotation will decrease D. the angular velocity will remain constant

Answer - Option C
Explanation -
In the absence of an external torque, the angular momentum is conserved,
i.e, I [latex]\omega[/latex] = constant
An increase in the value of moment of inertia (due to stretching of arms) will bring about a decrease in the value of speed of rotation of the turn table.

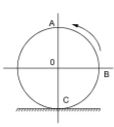
1. A boy twirls a 15 lb bucket of water in a vertical circle. If the radius of curvature of the path is 4 ft, determine the minimum speed the bucket must have when it is overhead at A so no water spills out

A. 11.35 [latex]\frac{ft}{s}[/latex] B. 0 C. 6.26 [latex]\frac{ft}{s}[/latex] D. 2.83 [latex]\frac{ft}{s}[/latex]

Answer - Option A
Explanation -
Centrifugal acceleration has to be equal to the do gravity acceleration (g)
[latex]\frac{{v}^{2}}{r} = g[/latex]
v = [latex]\sqrt{32.17 * 4} = 11.35 \frac{ft}{s}[/latex]
2. A 0.6 kg brick is thrown into a 25 kg wagon which is initially at rest. If, upon entering, the brick has a velocity of 10 m/s as shown, determine the final velocity of the wagon.

A. v = 0.203 m/s B. v = 0.208 m/s C. v = 0.240 m/s D. v = 0.234 m/s

Answer - Option A
Explanation -
The momentum in the horizontal direction remain same. So
[latex]{m}_{1}{v}_{1}cos(\theta) = ({m}_{1} + {m}_{2}){v}_{2}[/latex]
0.6 * 10cos (30º) = (0.6 +25)[latex]{v}_{2}[/latex]
v = 0.203 m/s
3. The friction experienced by a body, when in motion, is known as

A. rolling friction B. dynamic friction C. limiting friction D. static friction

Answer - Option B
Explanation -
Rolling friction - when body rolls.
Dynamic friction - when body moves.
Limiting friction - when body just to start move.
Static friction - when body doesn't move.
4. The bodies which rebound after impact are called

A. Perfectly inelastic bodies B. Perfectly elastic bodies C. neither Perfectly elastic nor Perfectly inelastic bodies D. None of these

Answer - Option B
Explanation -
If body rebounds with same velocity then it is perfectly elastic body. If body sticks with same velocity then it is perfectly inelastic body.
5. 30. The moment of inertia of a solid cone of mass m and base radius r about its vertical axis is

A. [latex]\frac{3m{r}^{2}}{5}[/latex] B. [latex]\frac{3m{r}^{2}}{10}[/latex] C. [latex]\frac{2m{r}^{2}}{5}[/latex] D. [latex]\frac{4m{r}^{2}}{5}[/latex]

Answer - Option B