Natural numbers:
1. Which of the following is a prime number ?

A. 33 B. 81 C. 93 D. 97

Answer: Option D Explanation: Clearly, 97 is a prime number.
Decimal Fractions:
1. The expression (11.98 x 11.98 + 11.98 x x + 0.02 x 0.02) will be a perfect square for x equal to:

A. 0.02 B. 0.2 C. 0.04 D. 0.4

Answer: Option C Explanation: Given expression = [latex](11.98)^{2}[/latex]+ [latex](0.02)^{2}[/latex] + 11.98 x x. For the given expression to be a perfect square, we must have 11.98 x x = 2 x 11.98 x 0.02 or x = 0.04
Percentages:
1. A fruit seller had some apples. He sells 40% apples and still has 420 apples. Originally, he had:

A. 588 apples B. 600 apples C. 672 apples D. 700 apples

Answer: Option D Explanation: Suppose originally he had x apples. Then, (100 - 40)% of x = 420. [latex]\frac{60}{100}[/latex]*x= 420 x = ([latex]\frac{420*100}{60}[/latex]) = 700
Profit & Loss:
1. If the selling price is doubled, the profit triples. Find the profit percent.

A. 66[latex]\frac{2}{3}[/latex] B. 100 C. 105[latex]\frac{1}{3}[/latex] D. 120

Answer: Option B Explanation: Let C.P. be Rs. x and S.P. be Rs. y. Then, 3(y - x) = (2y - x) y = 2x. Profit = Rs. (y - x) = Rs. (2x - x) = Rs. x. Profit % =([latex]\frac{x}{x}[/latex] * 100)% = 100%
Ratio & Proportion:
1. If 0.75 : x :: 5 : 8, then x is equal to:

A. 1.12 B. 1.2 C. 1.25 D. 1.30

Answer: Option B Explanation: x * 5 = (0.75 x 8) x = [latex]\frac{6}{5}[/latex] x = 1.20

LCM & HCF:
1. Six bells commence tolling together and toll at intervals of 2, 4, 6, 8 10 and 12 seconds respectively. In 30 minutes, how many times do they toll together ?

A. 4 B. 10 C. 15 D. 16

Answer: Option D Explanation: L.C.M. of 2, 4, 6, 8, 10, 12 is 120. So, the bells will toll together after every 120 seconds(2 minutes). In 30 minutes, they will toll together [latex]\frac{30}{2}[/latex] + 1= 16 times.
Quadratic Equations:
1. If the roots of a quadratic equation are 20 and -7, then find the equation?

A. [latex]x^{2}[/latex]+ 13x - 140 = 0 B. [latex]x^{2}[/latex]- 13x + 140 = 0 C. [latex]x^{2}[/latex]- 13x - 140 = 0 D. [latex]x^{2}[/latex]+ 13x + 140 = 0

Answer: Option C Explanation: Any quadratic equation is of the form [latex]x^{2}[/latex]- (sum of the roots)x + (product of the roots) = 0 ---- (1) where x is a real variable. As sum of the roots is 13 and product of the roots is -140, the quadratic equation with roots as 20 and -7 is: [latex]x^{2}[/latex]- 13x - 140 = 0.
Areas of squares:
1. The ratio between the perimeter and the breadth of a rectangle is 5 : 1. If the area of the rectangle is 216 sq. cm, what is the length of the rectangle?

A. 16 cm B. 18 cm C. 24 cm D. Data inadequate E. None of these

Answer: Option B Explanation: [latex]\frac{2(l + b)}{b}[/latex] = [latex]\frac{5}{1}[/latex] 2l + 2b = 5b 3b = 2l b = [latex]\frac{2}{3}[/latex] l Then, Area = 216 [latex] cm^{2}[/latex] l x b = 216 l * [latex]\frac{2}{3}[/latex] l = 216 [latex] l^{2}[/latex] = 324 l = 18 cm.
Volume and Surface Area:
1. A cistern 6m long and 4 m wide contains water up to a depth of 1 m 25 cm. The total area of the wet surface is:

A. 49 [latex]m^{2}[/latex] B. 50 [latex]m^{2}[/latex] C. 53.5 [latex]m^{2}[/latex] D. 55 [latex]m^{2}[/latex]

Answer: Option A Explanation: Area of the wet surface = [2(lb + bh + lh) - lb] = 2(bh + lh) + lb = [2 (4 x 1.25 + 6 x 1.25) + 6 x 4] m2 = 49 [latex]m^{2}[/latex].

Simple trigonometric identities:
1. In a triangle ABC, if angle A = 72°, angle B = 48° and c = 9 cm then Ĉ is

A. 60° B. 63° C. 66° D. 69°

Answer: Option C Explanation: 66°
heights and distances:
1. From a point P on a level ground, the angle of elevation of the top tower is 30°. If the tower is 100 m high, the distance of point P from the foot of the tower is:

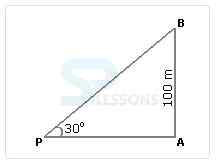
A. 149 m B. 156 m C. 173 m D. 200 m

Answer: Option C Explanation: Let AB be the tower

[latex]\frac{AB}{AP}[/latex]= tan 30°= [latex]\frac{AB}{AP}[/latex]=[latex]\frac{1}{\sqrt{3}}[/latex] AP = (AB x [latex]\sqrt{3}[/latex]) m = 100[latex]\sqrt{3}[/latex] m = (100 x 1.73) m = 173 m.
Volume and Surface Area:
1. 66 cubic centimeters of silver is drawn into a wire 1 mm in diameter. The length of the wire in metres will be:

A. 84 B. 90 C. 168 D. 336

Answer: Option A Explanation: Let the length of the wire be h. Radius =[latex]\frac{1}{2}[/latex]mm= [latex]\frac{1}{20}[/latex]cm,Then [latex]\frac{22}{7}[/latex]* [latex]\frac{1}{20}[/latex] * [latex]\frac{1}{20}[/latex] * h =66 h = [latex]\frac{66*20*20*7}{22}[/latex]= 8400 cm = 84 m
Collection and tabulation of statistical data
The following table gives the percentage of marks obtained by seven students in six different subjects in an examination.

1. What was the aggregate of marks obtained by Sajal in all the six subjects?

A. 409 B. 419 C. 429 D. 449

Answer: Option B Explanation: Aggregate marks obtained by Sajal = [ (90% of 150) + (60% of 130) + (70% of 120) + (70% of 100) + (90% of 60) + (70% of 40) ] = [ 135 + 78 + 84 + 70 + 54 + 28 ] = 449.